О развитии аппаратных средств статистического моделирования
В. М. Захаров, С. В. Шалагин
Введение
В развитии вычислительной техники существуют две тенденции - создание универсальных вычислительных машин и разработка проблемно-ориентированных специализированных устройств, ориентированных на эффективное решение определенного класса задач. Время показало, что существуют такие объекты и такие задачи, связанные с ними, что никакое повышение производительности универсальных вычислителей не позволяет надеяться на решение определенных задач в реальном масштабе времени.
Среди специализированных вычислительных устройств довольно давно (в 60-е годы прошлого столетия) возник класс устройств, спецификой которых является использование стохастических методов моделирования. Известный метод Монте-Карло был первым примером подобного подхода. В [1] представлена структурная схема проблемно-ориентированного специализированного устройства для аппаратной реализации метода Монте-Карло.
Для вычислений, опирающихся на идею стохастического подхода, характерен параллелизм глубокого уровня. Обычные вычислительные машины не могут его обеспечить, а при последовательном выполнении стохастических испытаний требования к быстродействию алгоритмов вычислений возрастают с ростом необходимой точности решения задачи квадратично. Практика вычислений свидетельствует о том, что есть задачи, которые другими методами либо не решаются, либо требуют чрезвычайно высокой производительности и больших затрат времени на поиск решения. Эти моменты с самого начала использования методов, опирающихся на статистические испытания, поставили задачу о создании специализированных вычислительных устройств, ориентированных на методы данной группы [2-5].
В дальнейшем появились и другие методы, опирающиеся на идею стохастического подхода: методы вероятностного представления информации, методы стохастической геометрии в распознавании образов, стохастические методы передачи данных и др. [6-12].
Цель доклада - представить результаты, характеризующие развитие специализированных аппаратных средств вычислительной техники, ориентированных на решение задач методами статистического моделирования и средств аппаратной поддержки методов вероятностного моделирования на вычислительных машинах (рассмотрение результатов не включает материал по иностранной библиографической литературе).
Аппаратные средства на основе вероятностных автоматов
Разработке вычислительных устройств, ориентированных на методы статистических испытаний и вероятностные алгоритмы, способствовало интенсивное развитие теории вероятностных автоматов в 60-70 годы и ее приложения к задачам синтеза и анализа вероятностных преобразователей и генераторов случайных процессов, представленное в [13-22], в том числе и в монографиях [13-18], в которых подытожены достижения теории
вероятностных автоматов по всем ее разделам, подробно изложены результаты по представимости языков и словарных функций в конечных вероятностных автоматах, вопросы гомоморфизма, эквивалентности и минимизации вероятностных автоматов, структурной теории, вероятностных грамматик, алгоритмов по исследованию автоматов в случайных средах и др.
Вероятностный автомат общего вида [13, 18] является математической моделью универсального преобразователя информации и в качестве автономного автомата служит математической моделью генератора широкого класса случайных последовательностей [13, 14, 18, 21]. Аппарат вероятностных автоматов имеет глубокую взаимосвязь с цепями Маркова, что позволяет решать задачи конечно-автоматного представления марковских последовательностей и функций цепей Маркова. На основные принципиальные вопросы, связанные с синтезом генераторов цепей Маркова, ответы получены на базе теоретико-автоматных идей [14, 16, 18, 21, 22]. Функции цепей Маркова рассматриваются как процессы, получаемые на выходе вероятностных моделей автоматного типа [18, 21]. Важность задачи их моделирования определяется широкими прикладными возможностями этих процессов [14-22].
Теория вероятностных автоматов определяет свойства и методы синтеза вероятностных устройств на достаточно высоком уровне абстракции. Поэтому решение задач, связанных с разработкой аппаратно- программных средств, математической моделью которых является вероятностный автомат, стимулировало развитие направления «аппаратной» поддержки выбранных автоматных вероятностных моделей. Технические аспекты этого направления связаны с задачей создания специализированных вероятностных процессоров, структура которых позволяет программным способом менять логику функционирования и реализовать различные вероятностные алгоритмы. Основополагающие результаты направления нашли отражение в ряде монографий [14, 23-25], в том числе в монографиях по проблемам синтеза генераторов случайных и псевдослучайных чисел [26-31] и в публикациях по разработкам разнообразных аппаратных средств для статистического моделирования [32-38]. Анализ патентной литературы показывает, что технические решения в области разработок по «аппаратной» поддержке защищены большим количеством авторских свидетельств, обширный список которых, в частности, представлен в [30, 31].
Развитию направления в значительной степени способствовало проведение в соответствии с планами конференций и совещаний Минвуза СССР и Научного совета АН СССР по комплексной проблеме «Кибернетика» трех всесоюзных симпозиумов по вероятностным автоматам и их приложениям:
- I Всесоюзный симпозиум по вероятностным автоматам и их приложениям, Казань, 1969, материалы симпозиума опубликованы в [39];
- II Всесоюзный симпозиум по вероятностным автоматам и их приложениям, Тбилиси, 1976, материалы симпозиума опубликованы в [40];
- III Всесоюзный симпозиум по вероятностным автоматам и их приложениям, Казань, 1983, который был организован Казанским государственным университетом им. Ульянова-Ленина и Казанским авиационным институтом им. А Н. Туполева, материалы симпозиума опубликованы в [41-43].
Материалы [39-43] , в том числе пленарные доклады III симпозиума: Бухараев Р.Г. «Некоторые методы и новые результаты в теории вероятностных автоматов» (Казань); Лоренц А.А. «Задачи структурного синтеза вероятностных автоматов» (Рига); Михайлов Г.А. «Математические модели случайных величин, процессов и полей» (Новосибирск); Альпин Ю.А., Захаров В.М. «Моделирование случайных последовательностей автономными автоматными схемами» (Казань); Фрейвалд Р.В. «Сравнение оценок сложности вычисления на вероятностных и детерминированных машинах» (Рига); Яровицкий Н.В. «Гармонические методы при исследовании поведения систем вероятностных автоматов» (Киев); Яковлев В.В., Федоров Р.Ф. «Некоторые методологические аспекты развития стохастических вычислительных устройств», отражают проблематику, степень участия различных организаций и научных школ и дают достаточно полное представление о состоянии в СССР в 70-80 годы исследований по вероятностным автоматами и их приложениям в области синтеза аппаратных средств статистического моделирования.
Вероятностные аппаратные средства на основе полиномиальной алгебры
В работах [44-45] определена взаимосвязь аппарата вероятностных автоматов и полиномиальных функций над полем Галуа вида G(n) = GF(2n) и предложен подход к решению задачи представления функций конечных цепей Маркова как задачи представления вероятностных автоматов на основе полиномиальной алгебры. В [44-51] разработаны методы построения полиномов с заданными свойствами над полем G(n) - полиномиальных моделей, порождающих различные виды цепей Маркова и заданные классы функций цепей Маркова. В качестве базиса для построения полиномиальных моделей применяются нелинейные полиномиальные функции (НПФ) от одной и от двух переменных над полем G(n) [44 - 45].
В поле Галуа эффективно реализуются системы потоковой обработки двоичных векторов большой размерности. Эго открывает возможность синтеза вероятностных автоматных моделей в однородных вычислительных сетевых структурах, допускающих параллельную реализацию. Перспективность этого направления определяется широким приложением функций конечных ЦМ и эффективностью арифметики конечных полей в задачах цифровой обработки информации.
Представление полиномиальных моделей в базисе ПЛИС/FPGA
В [51-57] разработаны теоретические основы структурного и функционального синтеза полиномиальных моделей генераторов дискретных стохастических процессов класса марковских и их функций в базисе программируемых логических интегральных схем (ПЛИС) класса FPGA. Решена актуальная проблема, связанная с генерированием и обработкой массивов вероятностных данных, представленных в цифровой форме и имеющих большую размерность, за ограниченный период времени, путем организации распределенных вычислений.
Для решения указанного класса задач эффективны распределенные вычислительные системы с программируемой архитектурой (РВС ПА), элементами которых являются сконфигурированные ПЛИС класса FPGA [58]. В настоящее время созданы РВС ПА различного назначения, выполненные при использовании унифицированных базовых модулей - многопроцессорных реконфигурируемых вычислителей на основе ПЛИС/FPGA. РВС ПА позволяют реализовать различные устройства вычислительной техники (ВТ), реконфигурируемые в реальном времени [58].
Развитие теоретических основ представления ВА на основе операций в конечных полях над потоками дискретных случайных величин открывает возможность для разработки эффективных методов синтеза на РВС ПА в базисе ПЛИС/FPGA генераторов дискретных стохастических процессов (ДСП) класса марковских и их функций на основе распределенного, непересекающегося по аргументам и адаптированного под архитектуру ПЛИС/FPGA вычисления значений НПФ от т переменных, определенных над конечным полем.
Создан общий метод синтеза [56, 57] при использовании однотипных специализированных цифровых вычислительных устройств, ориентированных на архитектуру ПЛИС/FPGA и описываемых НПФ над конечным полем, для генераторов дискретных стохастических процессов класса марковских и их функций. Для решения задачи синтеза (или создания прототипов) таких классов устройств ВТ как «система на кристалле», встраиваемые и портативные системы, широкое распространение получили IP-ядра (англ. Intellectual Properly) - готовые блоки, применяемые для проектирования микросхем и представленные на уровне абстрактного описания, на функциональном и на физическом уровнях. При ограничениях на быстродействие и размер занимаемой площади микросхемы, IP-ядра позволяют существенно ускорить процесс синтеза устройств ВТ на микросхемах, в том числе, на ПЛИС/FPGA.
Устройства, позволяющие вычислить НПФ от т переменных над полем G(n) вида
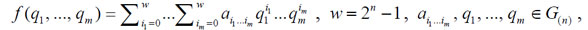
реализуемы на основе схем, альтернативных по оценкам временной и аппаратной сложности: параллельной, систолической, последовательностной [50] и параллельно-последовательностной [59]. Для этих структур получены оценки временной и аппаратной сложности [50, 59], равные соответственно
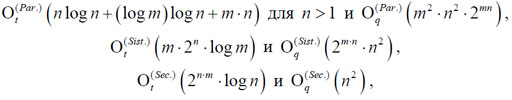
где в качестве меры сложности применяются операции над элементами поля GF(2).
Параллельно-последовательная схема есть схема вычисления значения НПФ вида (1) от т переменных над G(n) путем последовательного выполнения групп из d операций над G(n), выполняемых параллельно, вида:
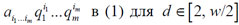
Оценки временной и аппаратной сложности для ППС занимают промежуточное положение между соответствующими оценками для параллельной и систолической схем, с одной стороны, и последовательностной схемой, с другой стороны [59].
Предложен метод синтеза устройств для вычисления дискретных детерминированных функций (ДДФ) от т переменных, представимой НПФ над G(n), на основе системы из l НПФ от т-l переменных каждая над полем G(k), п = к•l [60, 61]. Для ДДФ, представленной системой НПФ вида (1) над G(2) на основе параллельной реализации каждая, порядки оценок временной и аппаратной сложности составляют Ot (log2 (т·n)) и Oq(т • п • /2), 1 = п/к , соответственно (мера сложности - операции над GF(2)). Данное обстоятельство определяет преимущество в оценках временной сложности вычисления ДДФ системой НПФ (1) над G(2), примерно в n•(m + log2n)/log2(m•n) раз, по сравнению с соответствующими оценками для реализации указанной ДДФ при использовании параллельной схемы вычисления НПФ (1) над G(n} [60, 61].
Для решения задачи синтеза устройств ВТ на ПЛИС/FPGA, реализующих НПФ от т переменных над G(k) вида (1), применимы однотипные функциональные модули (ФМ), описываемые нелинейными полиномиальными преобразованиями над конечным полем [62-64], а для решения задачи аппаратного синтеза вероятностной части применимы ФМ, реализующие операции вычисления остатка по заданному модулю, отличного от степени числа два, над конечным полем [65-66].
В [67-68] показано, что перспективной является задача синтеза устройств для генерирования ДСП класса марковских и их функций на РВС ПА при использовании однотипных IP-ядер, описываемых на основе нелинейных полиномиальных преобразований над конечным полем. В соответствии с требованиями, предъявляемым к синтезируемым на РВС ПА устройствам по быстродействию и количеству задействованных процессорных элементов, актуальна задача адаптации указанных IP-ядер под архитектуру ПЛИС/FPGA.
Список литературы
- Бусленко Н.П. Метод статистических испытаний (Монте-Карло) и его реализация в цифровых машинах/ Н.П.Бусленко, Ю.А. Шрейдер - М.: Физматгиз, 1961. - 226 с.
- Голенко Д.И. Датчик случайных чисел к ЭВМ «Стрела» / Д.И.Голенко, В.П.Смирягин, В.Я.Капланский // Вопросы вычислительной техники. -М.: Машгиз, 1963. - С. 212-221.
- А.с. 212628 СССР, МПК G 06 F 15/36. Приставка к цифровым вычислительным машинам/ Р.Г. Бухараев // - 1968. Б.И. №9.
- Бухараев, Р.Г. Теория конструирования машин для статистического моделирования (Вероятностные автоматы): дис. ... д-ра техн. наук / Бухараев Раис Гатич. - Казань, 1968. - 307 с.
- Бухараев, Р.Г. Специализированная ЭВМ для моделирования и обработки функций конечных однородных цепей Маркова/ Р.Г. Бухараев, В.И. Геза// Всесоюз. симпозиум по вероятностным автоматам: тез. докл. - Казань: Изд-во КГУ, 1969.-С. 14-15.
- Кирьянов Б.Ф. Аппаратурные методы вычислений на основе стохастического принципа: дис. ... д-ра техн. наук / Кирьянов Борис Федорович. - Казань, 1973.
- Яковлев, В.В. Стохастические вычислительные машины / В.В. Яковлев, Р.Д. Федоров. - Л.: Машиностроение, 1974.-343 с.
- Кирьянов, Б.Ф. Основы теории стохастических вычислительных машин и устройств / Б.Ф. Кирьянов. - М. - 1976. - 168 с. - Деи. в ЦНИИТЭ приборостроения 21.05.1976, № 524.
- Федоров, Р.Ф. Стохастические преобразователи информации/ Р.Ф. Федоров, В.В. Яковлев, Г.В. Добрис. - Л.: Машиностроение, 1978. - 304 с.
- Федотов, Н.Г. Методы стохастической геометрии в распознавании образов / Н.Г. Федотов. - М.: Радио и связь, 1990.- 144 с.
- Бухараев Р.Г. Аппаратно-программная реализация методов стохастической геометрии в распознавании образов / Р.Г.Бухараев, Н.Р.Бухараев, В.М.Захаров и др.// Проблемы нелинейного анализа в инженерных системах: сб. трудов междунар. конф. -Казань: Изд-во КГТУ им. А.Н. Туполева. 1998. - т. 4,- Вьш.7. - С. 32-37.
- Осмоловский, С.А. Стохастические методы передачи данных / С.А. Осмоловский. -М.: Радио и связь, 1991. -240 с.
- Бухараев, Р.Г. Вероятностные автоматы/ Р.Г. Бухараев. - Казань: Изд-во КГУ, 1970. - 188 с.
- Поспелов, Д.А. Вероятностные автоматы / Д.А. Поспелов. - М.: Энергия, 1970. - 88 с.
- Лоренц, А.А. Синтез надежных вероятностных автоматов / А.А. Лоренц. - Рига: Зинатне, 1975. - 168 с.
- Лоренц, А.А. Надежность и быстродействие вероятностных автоматов/ А.А. Лоренц. - Рига: Зинатне, 1976. - 112 с.
- Бухараев, Р.Г. Вероятностные автоматы/ Р.Г. Бухараев. - Казань: Изд-во КГУ, 1977. - 247 с.
- Бухараев, Р.Г. Основы теории вероятностных автоматов/ Р.Г. Бухараев. - М.: Наука, 1985. - 287 с.
- Бухараев, Р.Г. Вероятностные автоматы //Теория вероятностей, математическая статистика, теоретическая кибернетика. -М.: ВИНИТИД982. Т.15. -С.79-122.
- Бухараев, Р.Г. Вероятностные автоматы и процессоры. М.: Знание, 1986. - № 6, - 48 с.
- Бухараев, Р.Г. Представимость языков и словарных функций, многотактных каналов и случайных последовательностей в конечных вероятностных автоматах: дис. ... д-ра физ.-математич. наук / Бухараев Раис Гатич. - Казань. 1981.
- Гиоргадзе, А.Х. Пространственно-временная декомпозиция и структурный анализ и синтез стохастических систем: дис. ... д-ра техн. наук/Гиоргадзе Анатолий Христофорович.-Тбилиси, 1981.-320с.
- Гладкий, В.С. Вероятностные вычислительные модели / В.С. Гладкий. - М.: Наука, 1973. - 300 с.
- Четвериков, В.Н. Вычислительная техника для статистического моделирования/ В.Н. Четвериков, Э.А. Баканович, А.В. Меньков. - М.: Сов. радио, 1978. - 312 с.
- Бухараев, Р.Г. Управляемые генераторы случайных кодов/ Р.Г. Бухараев, В.М. Захаров. - Казань: КГУ, 1978. - 160 с.
- Алексеев А.И. Теория и применение псевдослучайных сигналов/ А.И.Алексеев, А.Г.Шереметьев, Г.И.Тузов и др. - М.: Наука, 1969. - 367 с.
- Ярмолик В.Н. Генерирование и применение псевдослучайных сигналов в системах испытаний и контроля/ В.Н. Ярмолик, С.Н. Демиденко - Минск: Наука и техника, 1986. - 200 с.
- Винокуров, В.И. Дискретно-кодированные последовательности/ В.И. Винокуров, В.Е. Гантмахер. - Ростов н/Д: РГУ, 1990.-288 с.
- Иванов, М.А. Теория применения и оценка качества генераторов псевдослучайных последовательностей / М.А. Иванов, И.В. Чугунков. -М.: КУДИЦ-ОБРАЗ, 2003.-240 с.
- Песопшн, В.А. Генераторы псевдослучайных и случайных чисел на регистрах сдвига / В.А. Песопшн, В.М. Кузнецов. - Казань: Изд-во КГТУ им. А.Н. Туполева, 2007. - 296 с.
- Кузнецов, В.М. Генераторы случайных и псевдослучайных последовательностей на цифровых элементах задержки: монография/ В.М. Кузнецов, В.А. Песопшн. - Казань: Изд-во Казан, гос. техн. ун-та, 2013. - 336 с.
- Песопшн В.А. Устройство ввода случайных чисел ЕС-6903/ В.А.Песопшн// Вероятностные автоматы и их приложения: сб. трудов. - Казань: Изд-во КГУ, 1986. - С.22-29.
- Песопшн, В.А. Устройства вычислительной техники для генерирования случайных и псевдослучайных последовательностей и чисел: дис. ... д-ра техн. наук/.Песопшн.Валерий Андреевич - Казань, 1987. - 408 с.
- Баканович Э.А. Статистический процессор для автоматизированных систем испытаниями и моделированием/ Э.А.Баканович, Н.А.Волорова// Управляющие системы и машины, 1986. - № 1. -С. 90-95.
- Пех X. Теория построения стохастических устройств для реализации статистических испытаний: автореф. дис. ... д-ра техн. наук/ Пех Хенрик. - Ленинград, 1990. - 31 с.
- Захаров, В.М. Аппаратно-программная организация специализированных процессоров на основе автономных вероятностных автоматов: автореф. дис. ... д-ра техн. наук/ Захаров Вячеслав Михайлович. - Казань, 1995. - 30 с.
- Глова В.И. Вычислительные средства для статистического моделирования: автореф. дис. ... д-ра техн. наук/ Глова Виктор Иванович. - Казань, 1995. - 33 с.
- Песошин, В.А. Аппаратно-программные системы статистического моделирования и защиты информации /В. А. Песошин, В.М. Захаров, В.М. Кузнецов и др. // Проблемы и перспективы развития информационных технологий: материалы докл. Всерос. науч.-техн. конф. 10 февр. 2012. - Казань: Изд-во Казан, гос. техн. ун-та, 2012. - С. 8-21.
- Сб. Вероятностные автоматы и их применения. - Рига: “Зинатне”, 1971,- №1. -160 с.
- Материалы II Всесоюзного симпозиума по вероятностным автоматам и их приложениям. - Тбилиси: «Мецниере- ба», 1976.- 153 с.
- Тезисы докладов III Всесоюзного симпозиума по вероятностным автоматам. - Казань: Изд-во КГУ, 1983. - 140 с.
- Бухараев Р.Г., Захаров В.М. Всесоюзный симпозиум по вероятностным автоматам и их приложениям/ Р.Г.Бухараев, В.М.Захаров// Науч. совет по проблеме «Кибернетика»: сб. информационных материалов. -1 (133).- М: Изд-во АН СССР, 1984. - С.3-10.
- Сб. Вероятностные автоматы и их приложения. Под редакцией Р.Г. Бухараева / Составитель В.М. Захаров - Казань: Изд-во КГУ, 1986. - 214 с.
- Захаров,В.М. Синтез автономных вероятностных автоматов на основе полей Галуа / В.М.Захаров, Ш.Р. Нурутдинов, С.В. Шалагин // Сб.Исследования по информатике. - Казань: Изд-во ИЛИ АН РТ, 2000. - Выл. 2.-С. 107-116.
- Захаров, В.М. Полиномиальное представление цепей Маркова над полем Галуа/ В.М. Захаров, Ш.Р. Нурутдинов, В. В. Шалагин//Вестник КГТУ им. А.Н.Туполева. -2001. -№ 3. - С. 27-31.
- Захаров, В.М. Полиномиальное представление конечно-автоматных случайных последовательностей над полем Галуа / В.М. Захаров, Ш.Р. Нурутдинов, С.Ю. Соколов и др. // Вестник КГТУ им. А.Н. Туполева. - 2003. - № 2. - С. 24-28.
- Нурутдинов Ш.Р. Основы теории полиномиальных моделей автоматных преобразований над полем Галуа - Казань: КГУ, 2005.- 156 с.
- Эминов Б.Ф. Методы и алгоритмы построения и анализа полиномиальных функций над конечным полем на основе стохастических матриц: автореф. дис. ... канд. физ.-математич. наук/ Эминов Булат Фаридович - Казань, 2008. - 20 с.
- Захаров, В.М. Параллельные марковские модели над полем GF(2n) / В.М. Захаров, С.В. Шалагин // Высокопроизводительные параллельные вычисления на кластерных системах: тез. докл. 8-й Междунар. конф. 17 - 21 нояб. 2008. - Казань: Изд-во КГТУ им. А.Н. Туполева, 2008. - С. 155-160.
- Шалагин, С.В. Полиномиальные модели генераторов дискретных случайных величин / С.В. Шалагин // Инфоком- муникационные технологии Глобального информационного общества: сб. тр. 6-й ежегодной Междунар. науч.- практ. конф. 4-5 сент. 2008. - Казань: Центр Оперативной Печати, 2008. - С. 159-171.
- Захаров В.М. Методы и алгоритмы построения и анализа полиномиальных функций над конечным полем на основе стохастических матриц/ В.М.Захаров, Б.Ф.Эминов. - Saarbriicken Germany: LAP Lambert Academic Publishing GmbH & Co. KG, 2011. - 168 c.
- Захаров, В.М. Метод моделирования и преобразования функций цепей Маркова в полях Галуа и его реализация в базисе ПЛИС/ В.М. Захаров, Ш.Р. Нурутдинов, С.В. Шалагин// Методы и средства обработки информации: тез. докл. 2-й Всерос. науч. конф. 5-7 окт. 2005 - М.: МГУ, 2005. - С. 256-262.
- Захаров, В.М. Реализация полиномиальных моделей над полем GF(2An) неоднородных цепей Маркова и их функций в базисе ПЛИС/FPGA/ В.М. Захаров, Ш.Р. Нурутдинов, С.В. Шалагин// Инфокоммуникационные технологии глобального информационного общества: тез. докл. 4-й ежегодной Междунар. науч.-практ. конф. 5-8 сент. 2006. - Казань: Центр инновационных технологий, 2006. - С. 62-66.
- Захаров, В.М. Полиномиальные модели генераторов дискретных марковских процессов в базисе ПЛИС/FPGA / В. М. Захаров, С.В. Шалагин // Проблемы техники и технологий телекоммуникации: тез. докл. 9-й Междунар. науч.-техн. конф. 25-27 нояб. 2008. - Казань: Изд-во КГТУ им. А.Н. Туполева, 2008. - С. 90-91.
- Шалагин, С.В. Представимость дискретных детерминированных нелинейных функций на основе многочленов над полем Галуа в базисе ПЛИС класса FPGA / С.В. Шалагин. - Казань: Изд-во КГТУ им. А.Н. Туполева, 2010.-184 с.
- Шалагин, С.В. Представление нелинейных полиномиальных функций над полем Галуа в базисе ПЛИС/FPGA/ С. В. Шалагин. - Saarbriicken Germany: LAP Lambert Academic Publishing GmbH & Co. KG, 2012. - 188 c.
- Шалагин С.В. Методы синтеза устройств вычислительной техники на основе нелинейных полиномиальных функций над конечным полем: автореф. дис. ... докт. техн. наук/ Шалагин Сергей Викторович. - Казань, 2013. - 32 с.
- Каляев, И.А. Реконфигурируемые мультиконвейерные вычислительные структуры / И.А. Каляев, И.И. Левин, Е.А. Семерников и др. - 2-е изд. - Ростов н/Д: Изд-во ЮНЦ РАН, 2009. - 344 с.
- Шалагин, С.В. Цифровые вычислительные устройства полиномиальной функции на основе однотипных операций над полем Галуа/ С.В. Шалагин // Проблемы и перспективы развития информационных технологий: материалы Всерос. науч.-техн. конф. 10 февр. 2012. - Казань: Изд-во Казан, гос. техн. ун-та, 2012. - С. 63-73.
- Шалагин, С.В. О представлении нелинейных полиномов над конечным полем распределенной вычислительной системой/ С.В.Шалагин// Нелинейный мир - 2009,- № 5. - С.376-379.
- Шалагин, С.В. Представимость неоднородных цепей Маркова и их стохастических функций полиномами от нескольких переменных над полем Галуа / С.В. Шалагин// Инфокоммуникационные технологии Глобального информационного общества: сб. тр. 7-й ежегодной Междунар. науч.-практ. конф. 10-11 сент. 2009. - Казань: Центр оперативной печати, 2009. - С. 134-139.
- Захаров, В.М. Аппаратная реализация умножения элементов поля Галуа на программируемых микросхемах архитектуры FPGA/ В.М.Захаров, Ш.Р. Нурутдинов, С.В.Шалагин// Вестник КГТУ им.А.Н.Туполева. - 2001.- № 1.- С.36 - 47.
- Shalagin, S.V. Computer Evaluation of a Method for Combinational-Circuit Synthesis in FPGAs / S.V. Shalagin // Russian Microelectronics. - 2004. - Vol. 33; № 1. - P. 46-54.
- Шалагин, C.B. Умножение элементов расширений полей Галуа в базисе ПЛИС/FPGA/ С.В. Шалагин // Информационные технологии. - 2007. - № 12. -С.22-27.
- Захаров, В.М. Алгоритм вычисления остатка по модулю и оценки его сложности/ В.М.Захаров, Е.Л.Столов, С.В.Шалагин// Информационные технологии. - 2010. - № 11. - С. 32 - 36.
- Пат. 2421781 РФ МПК8 G06F 7/72, Н03М 7/18. Устройство для формирования остатка по заданному модулю/ В.М.Захаров, Е.ЛСтолов, С.В.Шалагин; заявитель и патентообладатель ГОУ ВПО Казан, гос. техн. ун-т. - № 2009138613/08; заявл. 19.10.2009; опубл. 20.06.2011, Бюл. № 17. - 12 с.: ил.
- Шалагин, С.В. Реализация устройств вычислительной техники на многопроцессорных системах с программируемой архитектурой / С.В. Шалагин // Вестник МарГТУ. - 2011. - № 1 (11). - С. 38—46.
- Шалагин, С.В. Моделирование дискретных марковских процессов на распределенной вычислительной системе с программируемой архитектурой/ С.В. Шалагин // Динамика нелинейных дискретных электротехнических и электронных систем: материалы 10-й Всерос. науч.-техн. конф. 6-8 июня 2013. - Чебоксары: Изд-во Чуваш, ун-та, 2013.-С. 60-61.
Об авторе: Казанский национальный исследовательский технический университет им. А.Н. Туполева-КАИ
Казань, Россия
gilvv@mail.ru, sshalagin@mail.ru
Материалы международной конференции Sorucom 2014 (13-17 октября 2014)
Помещена в музей с разрешения авторов
9 января 2015
