О некоторых пионерских работах на первых ЭВМ
Ю. Л. Кетков
Машина ГИФТИ и схема Горнера
Первый выпуск математиков-вычислителей в Горьковском университете состоялся в 1957 году благодаря поддержке со стороны д.ф.-м.н. А.А. Ляпунова в то время зав. отделом программирования Отделения прикладной математики Математического института им. В.А. Стеклова АН СССР. Он же одновременно был профессором мехмата МГУ. Весь учебный 1956–1957 год шесть студентов физмата ГГУ провели в Москве, т.к. компьютеров в Горьковской области, включая и всемогущий ВНИИЭФ (г.Саров), еще не было. Мы посещали в МГУ лекции по программированию, которые начал читать молодой аспирант А. П. Ершов, проходили годичную стажировку на первых цифровых ЭВМ М-2 (в лаборатории И.С. Брука), БЭСМ (в ИТМиВТ), Стрела-1 (в ОПМ МИ АН СССР), выполняли дипломные работы. Почти весь наш выпуск был по распределению направлен на работу в Горьковский Исследовательский Физико-технический Институт (ГИФТИ при ГГУ), где в это время создавался первый в Горьковской области вычислительный центр (ВЦ ГИФТИ).
Поначалу главным средством вычислений была самая мощная аналоговая машина МН-8, которая обеспечивала решение систем дифференциальных уравнений высокого порядка. Она было очень важным подспорьем для специалистов по теории колебаний, которые занимались исследованием процессов управления и устойчивостью работы ядерных реакторов, проектировавшихся для первых АЭС и атомных подводных лодок. Одновременно заканчивалась настройка небольшой цифровой ЭВМ, получившей название «Машины ГИФТИ». Она разрабатывалась группой выпускников кафедры теории колебаний радиофизического факультета ГГУ, долгое время возглавляемой академиком А.А. Андроновым. В свое время А.А. Андронов был членом межведомственных комиссий, проверявших работу ряда академических подразделений, связанных с проектированием первых ЭВМ в нашей стране. Он здраво оценил перспективность нового направления и всячески содействовал развитию этой тематики на своей кафедре.
В отличие от ЭВМ «Стрела-1», занимавшей в ОПМ двухэтажное здание и его подвальные помещения, с обслуживающим персоналом более 200 человек машина ГИФТИ спокойно размещалась в небольшой комнате и потребляла около 15 квт электроэнергии. Она была машиной последовательного действия с оперативной памятью в 2016 тридцатидвухразрядных ячеек, расположенных на магнитном барабане. На этом же барабане были реализованы сверхбыстрые рециркуляционные регистры, позволившие довести скорость работы арифметического устройства до 6000 сложений в сек. Операции деления-умножения, естественно, выполнялись примерно в 30 раз медленнее. Общая производительность машины ГИФТИ сдерживалась медленной оперативной памятью и в среднем составляла около 100 операций в сек.
Трое первых программистов, включая автора, были нацелены на создание базового программного обеспечения – тестовое хозяйство, библиотеки стандартных функций, простейшие методы решения алгебраических и дифференциальных уравнений. Скорость вычислений была для нас главным критерием качества программ. Особенно удручала небольшая скорость выполнения операций деления-умножения. Поэтому первой пионерской работой, позволившей на 25% ускорить работу подпрограмм вычисления элементарных функций, была борьба с традиционной схемой Горнера. Как правило, для вычисления значений элементарных функций использовались полиномы 8–10 степени, полученные тем или иным способом (разложение в ряд Тейлора, непрерывные дроби, снижение старших степеней за счет полиномов Чебышева и т.п.). Схема Горнера позволяла вычислить значение полинома n-ой степени в заданной точке за n операций умножения и n операций сложения:
Pn(x) = an•xn + an-1•xn-1 + … + a1•x + a0
Pn(x) = (…((an•x + an-1)•x + … + a1)•x + a0
Её оптимальность сомнений не вызывала: чтобы задействовать n+1 независимых коэффициентов ai без n сложений никак нельзя было обойтись. А по поводу умножений сомнения возникали – обязательно ли было каждым умножением повышать степень промежуточного результата только на 1. Ведь из алгебры известно, что полином можно представить в виде произведения скобок, содержащих выражения вида (x xj ) , где xj – корни полинома. В том случае, когда один из корней оказывался комплексным (xj = c + i•d), для него всегда находился сопряженный (c i•d) , и произведение двух парных скобок заменялось вещественным полиномом 2-й степени. Дело было за малым – надо найти все корни полинома (и всё это ради только того, чтобы вычислить значение полинома при заданном аргументе x). Из той же алгебры следовало, что полиномы выше 4-й степени в радикалах неразрешимы. Следовательно, надо было находить корни приближенным способом и исследовать распространение ошибок первого шага на общую погрешность вычисления полинома. По сравнению с этим схема Горнера казалась блестящей находкой (и даже сегодня многие в этом уверены). Гораздо более перспективным казался путь, подсказанный публикацией статьи американского математика Дж.Тодда [1], где со ссылкой на работу [2] была приведена частная схема вычисления полинома 6-й степени с повышением степени промежуточного результата на 2 при каждом умножении. Эта схема требовала предварительного пересчета исходных коэффициентов (a6 , a5 , a4 , a3 , a2 , a1, a0) в 6 других также независимых коэффициентов (b6 ,b5 ,...,b0) и позволяла сэкономить 2 умножения. Все было бы хорошо, если бы на стадии пересчета при некоторых комбинациях исходных коэффициентов не получались бы квадратные уравнения, не имевшие вещественных корней. А появление комплексных коэффициентов bj сводило на нет все преимущества схемы Тодда.
В 1957 году мне удалось придумать более универсальную схему, напоминающую американский аналог, но для повышения степени промежуточного полинома на 2 она требовала через шаг то одного умножения, то двух. Зато пересчет исходных коэффициентов никогда не приводил к комплексным j b . По сравнению со схемой Горнера экономия в количестве умножений составила 25 %. Предварительные затраты на пересчет исходных коэффициентов во внимание принимать не надо, т.к. эти затраты разовые, а все последующие обращения к подпрограмме вычисления стандартной функции выполнялись по укороченной схеме. Свою первую апробацию новые стандартные программы прошли на машине ГИФТИ. Впервые эта схема была опубликована в 1958 году в относительно мало известном для программистов журнале «Известия вузов. Радиофизика» [3], а позднее по рекомендации Л.А.Люстерника она была включена в один из сборников «Справочной Математической Библиотеки» (СМБ, [4]).
УИС РГМ – прообраз первых электронных таблиц на ЭВМ типа М-20
8 марта 1961 года в ВЦ ГИФТИ была введена в эксплуатацию одна из лучших ЭВМ первого поколения М-20. После этого машина ГИФТИ была передана кафедре теории колебаний радиофакультета в качестве средства расширения материальной базы учебного процесса. Перед группой программирования, переключившейся на М20 и насчитывающей уже порядка 15 человек, были поставлены задачи поиска внешних заказчиков и повышения квалификации в области решения разнообразных прикладных задач. Довольно стабильным поставщиком задач, связанных с управлением атомными реакторами, была специализированная лаборатория ГИФТИ, возглавляемая Н.А.Железцовым. В силу специфики тематики она выступала как организация «п/я 88». Затем к нам потянулись радиофизики, специалисты по строительной механике, конструкторы новых радиолокационных станций. В начале 1963 года к руководству ВЦ обратился главный инженер ЦКБ «Волгобалтсудопроект» А.А.Брайловский с просьбой помочь в выполнении плазовых расчетов для сухогруза типа «река-море» (проект 1829) по схеме, разработанной в НИИ Технологии Машиностроения (НИИТМ, Ростов-на-Дону). Автором этой схемы был главный конструктор СКБ НИИТМ Д.С. Китаинов, а сама технология образмеривания всех практических сечений корпуса судна носила название радиусографического метода. Название метода объясняется тем, что все продольные (ватерлинии, батоксы) и поперечные (шпангоуты) сечения проектируемой поверхности формировались из отрезков прямых и дуг окружностей. На большинстве участков судовой поверхности они сопрягались с сохранением значения первой производной на линиях стыков.
Для того чтобы пояснить суть расчетов по радиусографическому методу, опишем некоторые элементы технологии проектирования судов и предварительной подготовки чертежной документации на судостроительных заводах нашей страны. Два крупнейших центра по проектированию надводных и подводных судов располагались в городах Горький и Ленинград. В их составе насчитывалось около десятка специализированных конструкторских бюро, которые в соответствии с техническими заданиями разрабатывали проекты конкретных изделий. Наряду с уточненными тактико-техническими данными корабля, составом и размещением его оборудования основу проекта составлял теоретический чертеж судовой поверхности, выполненный в трех взаимно перпендикулярных плоскостях. Сотрудники КБ составляли такие чертежи в масштабе от 1:25 до 1:100 в зависимости от размера судна. Как правило, на чертеже, поступившем из КБ, были представлены поперечные сечения судна в виде 21 теоретического шпангоута. Продольных сечений (ватерлинии, батоксы) было существенно меньше. Особое внимание уделялось сечениям, характеризующим главные измерения судна (мидель-шпангоут, грузовая ватерлиния и др.). Одна из проекций с поперечными сечениями носа и кормы показана на рис. 1
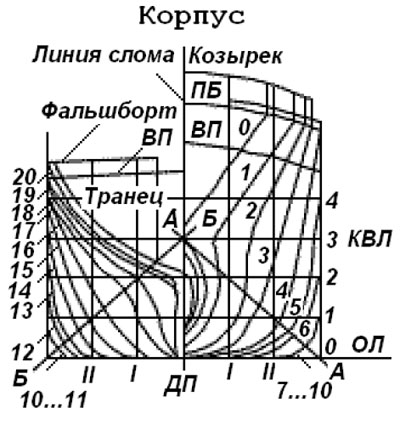
Рис.1. Проекция «Корпус»
Теоретический чертеж неминуемо сопровождался большим количеством неточностей, нестыковкой координат одних и тех же точек судовой поверхности на разных сечениях. Ошибка в 1 мм с теоретического чертежа увеличивалась до 10 см на реальной поверхности. Поэтому графические данные теоретического чертежа обязательно проходили согласование в процессе плазово-разметочных работ, выполняемых в специальных (плазовых) цехах судостроительных предприятий. Так, например, плазовый цех Сормовского судостроительного завода представлял собой одноэтажное здание длиной порядка 200 м с идеально выровненным полом. На этом полу несмываемой тушью в натуральную величину воспроизводились все элементы теоретического чертежа с добавлением нужного количества промежуточных сечений. Плавность линий достигалась на глаз с помощью специальных гибких реек («правил», в англоязычной терминологии – «сплайнов»), которые прижимались в опорных точках металлическими грузиками («крысами») в форме небольших утюжков. Линия считалась идеальной, если после снятия нагрузки рейка сохраняла приданную ей форму и отклонялась в опорных точках не более чем на 1–2 мм. Субъективизм в построении плавных линий приводил к тому, что плазовые чертежи одного и того же проекта, выполненные на разных судостроительных заводах, слегка отличались. Поэтому ремонт судна всегда должен был выполняться на том заводе, где корабль был построен.
Основу радиусографического метода составлял так называемый радиусографический ключ – набор небольшого количества продольных линий, которые проходили вдоль корпуса судна и сами были составлены из отрезков прямых и дуг окружностей. Некоторые линии ключа были расположены на поверхности судна. Точки ключевых линий определяли опорные точки на судовой поверхности и координаты центров всех дуг, образующих поперечные сечения. Построение ключа велось обычно от прототипа изделия и определялось пространственным воображением и опытом проектировщика. Д.С. Китаинов виртуозно владел технологией формирования радиусографических ключей, но с большой неохотой передавал свой опыт другим проектировщикам. После того, как радиусографический ключ был сформирован, наступал весьма кропотливый и трудоемкий процесс вычисления координат всех точек сопряжения смежных отрезков и дуг окружностей, радиусов закруглений на каждом из практических сечений. Для этой цели в СКБ НИИТМ было сформировано две библиотеки соответствующих геометрических процедур, каждая из которых содержала порядка 40 типовых геометрических задач и численных схем их решения. Разница между библиотеками заключалась только в форме задания уравнения прямой (через угловой коэффициент или через пару точек). Таким образом, задача построения согласованных плазовых таблиц сводилась к многократному выполнению формируемых цепочек геометрических задач. Но автоматизировать этот процесс сотрудникам НИИТМ никак не удавалось. Оказались несостоятельными и те немногие организации Ростова-на-Дону, которые располагали средствами вычислительной техники. А сотрудникам ВЦ ГИФТИ, получившим начальную подготовку в одном из лучших вычислительных центров страны и успешно осваивавших идеи М.Р. Шура-Буры, заложенные в интерпретирующей системе ИС-2 [6], удалось за год построить несколько версий универсальных интерпретирующих систем радиусографического метода.
Основной идеей построения «матричных систем программирования» послужила мысль об объединении формата команды трехадресной вычислительной машины М-20 и способа задания форматов исходных данных для процедур, включенных в состав библиотеки ИС-2.
|
π |
КОП |
A1 |
A2 |
A3 |
π – признаки модификации адресов (3 бита, одна восьмеричная цифра);
КОП – код операции (две восьмеричные цифры);
А1, А2 – адреса первого и второго операндов (по четыре восьмеричные цифры);
А3 – адрес результата операции (четыре восьмеричные цифры).
|
π |
16 |
*+1 |
7501 |
7610 |
|
|
|
Apar1 |
Nсп |
Apar2 |
Обращение к процедуре с номером Nсп.
16 – команда передачи управления на точку входа в ИС-2 (ячейка с адресом 7501);
7610 – ячейка, в которой формируется команда возврата по адресу *+1, т.е. по адресу команды, содержащей вторую строку обращения;
Apar1, Apar2 – адреса данных, необходимые для работы вызываемой процедуры.
Абстрактный формат «команды матричного программирования» должен был выглядеть следующим образом:
|
Asource |
KMO |
Adest |
Asource – адрес (номер) строки в матрице исходных данных
KMO – код матричной операции
Adest – адрес (номер) строки в матрице результатов
Анализируя состав библиотек с геометрическими построениями, мы обнаружили, что в каждой из задач количество исходных данных не превосходило восьми. Поэтому в качестве длины строки исходных данных была принята цифра 8, а сами исходные значения адресовались одной восьмеричной цифрой – от 0 до 7. Полный адрес любой компоненты исходных данных идентифицировался четверкой восьмеричных цифр, первые три из которых соответствовали номеру строки в «матричной программе», а младшая определяла порядковый номер аргумента в соответствующем векторе исходных данных. С тем, что в ряде процедур количество исходных данных было заведомо меньше восьми, мы смирились, т.к. единообразие в адресации для нас было важнее. Примерно так же обстояло и дело со стандартизацией формата строк матрицы результатов – во всех задачах их количество не превышало трех.
Было совершенно очевидно, что набор кодов матричных программ не исчерпывался только задачами геометрических построений. Нужно было подключить логику (условные и безусловные переходы), команды организации циклов, команды ввода и вывода исходных данных.
Матричная программа для расчета поперечных или продольных сечений представляла собой циклически повторяющийся список геометрических построений, разбитый на два раздела. В первом разделе для каждого значения циклически повторяющейся координаты (x – для шпангоутов, y – для батоксов, z – для ватерлиний) по соответствующим фрагментам ключевых линий определялись координаты опорных точек и центров дуг, образующих текущее сечение. Полученные результаты засылались в соответствующие клетки матрицы исходных данных второго раздела, где была закодирована последовательность геометрически процедур, вычислявших геометрические параметры продольного или поперечного сечения. После того, как аналитика сечения была рассчитана, с заданным шагом вычислялись плазовые координаты точек, расположенных на данном сечении. На небольшом примере поперечного сечения (рис. 2) продемонстрируем технологию задания соответствующего фрагмента матричной программы.
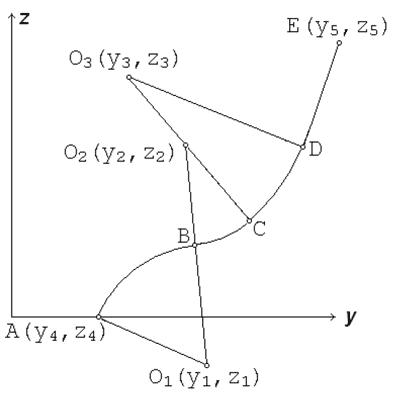
Рис.2. Схема шпации. Центры окружностей O1,O2,O3 расположены на продольных линиях радиусографического ключа. Точки A и E находятся на ключевых линиях, проложенных по поверхности судна. Координаты точек сопряжения B, C и D должны быть вычислены по соответствующей цепочке геометрических задач
В табл.1 приведена запись последовательности геометрических построений и соответствующих исходных данных, которые готовил проектировщик формы судовой поверхности. С целью сокращения объема таблицы данные по расчету ключевых параметров уже занесены в соответствующие позиции в виде конкретных числовых значений.
Таблица 1.
|
№ строк |
Исходные данные |
Nсп |
Выдача на печать |
Дальнейшая адресовка | |||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
4 |
2 |
1 |
4 |
2 |
1 | ||
|
1 |
20 |
-10 |
15 |
0 |
|
|
|
|
12 |
|
|
R1 |
|
|
31, |
|
2 |
20 |
-10 |
22 |
30 |
|
|
|
|
12 |
|
|
n1 |
|
|
125 |
|
3 |
n1 |
R1 |
|
|
|
|
|
|
41 |
|
|
R2 |
|
|
30 |
|
4 |
22 |
30 |
12 |
49 |
|
|
|
|
12 |
|
|
n2 |
|
|
51, |
|
5 |
n2 |
R2 |
|
12 |
49 |
R3 |
|
|
40 |
|
zD |
R3 |
|
73 |
135 |
|
6 |
60 |
72 |
yD |
zD |
|
|
|
|
16 |
|
b |
yD |
|
121 |
50 |
|
7 |
60 |
72 |
22 |
30 |
-10 |
R1 |
-1 |
|
02 |
|
b1 |
k |
|
131 |
65 |
|
10 |
20 |
-10 |
22 |
30 |
30 |
R2 |
+1 |
|
02 |
|
b2 |
k1 |
|
|
72 |
|
11 |
19 |
49 |
|
20 |
|
|
|
|
02 |
|
zB |
k2 |
|
|
120 |
|
12 |
k1 |
b1 |
|
22 |
|
|
|
|
70 |
|
zC |
yB |
|
|
130 |
|
13 |
k2 |
b2 |
|
|
|
|
|
|
70 |
|
|
yC |
|
|
|
Перенос содержимого этой таблицы на бланки матричных программ осуществляется почти механически. Эквивалент табл.1 в формате, пригодном для ввода в ЭВМ, имеет следующий вид (табл.2).
Таблица 2
|
№ |
Код |
Адрес |
Рассылка |
Комментарий |
|
1 |
12 |
0010 |
|
Вычисление и печать R1 |
|
1 |
|
|
0031 |
Засылка R1 |
|
1 |
12 |
0020 |
0125 |
« – « – « |
|
1 |
41 |
0030 |
0030 |
Вычисление и печать n1 |
|
1 |
|
|
0051 |
Засылка n1 |
|
1 |
12 |
0040 |
0135 |
Вычисление и печать R2 |
|
1 |
40 |
0050 |
0050 |
Засылка R2 |
|
1 |
16 |
0060 |
0065 |
« – « – « |
|
1 |
|
|
0073 |
Вычисление и печать n2 |
|
1 |
02 |
0070 |
0072 |
Засылка n2 |
|
1 |
02 |
0100 |
|
Вычисление и печать R3 |
|
1 |
|
|
0121 |
Засылка R3 |
|
3 |
02 |
0110 |
0120 |
Вычисление и печать zD , yD |
|
2 |
|
|
0131 |
Засылка zD |
|
1 |
70 |
0120 |
0130 |
Засылка yD |
|
3 |
70 |
0130 |
|
Вычисление и печать b, k |
|
3 |
|
|
|
Вычисление и печать b1 , k1 |
|
2 |
|
|
|
Засылка b1 |
|
1 |
|
|
|
Засылка k1 |
|
3 |
|
|
|
Вычисление и печать b2 , k2 |
|
2 |
|
|
|
Засылка b2 |
|
1 |
|
|
|
Засылка k2 |
|
3 |
|
|
|
Вычисление и печать zB , yB |
|
3 |
|
|
|
Вычисление и печать zC , yC |
Первые две версии интерпретирующих систем УИС РГМ и УИС РГВ отличались только наборами библиотечных процедур. Третья версия была пополнена операциями развертки листов судовой обшивки. Первая публикация по технологии автоматизации радиусографического метода [5] носила закрытый характер, т.к. ряд проектов, по которым были выполнены расчеты плазовой документации, относились к оборонной промышленности. Первая открытая публикация появилась два года спустя [7]. Тем не менее, прототип электронных таблиц на отечественных ЭВМ появился примерно за 15 лет до официального представления системы VisiCalc. Цифровая индексация клеток матричной программы была мерой вынужденной, т.к. алфавитно-цифровые устройства подготовки данных в нашей стране еще не производили. Всего в ВЦ ГИФТИ за период с 1963 по 1965 гг были проведены плазовые расчеты по 19 надводным судам. Автор причастен к внедрению разработанных комплексов в ряде организаций авиационной и судостроительной промышленности.
Первые линейные сплайны
Попытки визуализации результатов графо-аналитических построений привели нас к использованию первых перьевых плоттеров. Усовершенствование управления их пишущим узлом начинались с того, что сначала перо могло перемещаться на минимальный шаг в одном из четырех направлений. Затем поворот на угол, кратный 90º, был заменен перемещениями под углом, кратным 45º. Наконец, графопостроители начали снабжать интерполяторами, сначала только линейными, а позднее – линейно-круговыми. Это позволило в программе управления плоттером задавать величину перемещения, кратную нескольким минимальным шагам по каждой из координат. В связи с этим возникла задача построения оптимального алгоритма кусочно-линейной аппроксимации произвольного криволинейного контура. И формулировалась-то она предельно просто: как далеко можно было шагнуть вдоль кривой, чтобы соответствующая хорда отклонилась от исходной линии не более чем на заданную величину. Для дуг окружностей существует аналитическая формула, связывающая длину хорды со стрелкой прогиба. А что делать с другими кривыми, например с эллиптическими или параболическими? А если исходная кривая задана таблично? Идентичная задача была актуальной и для станков с числовым программным управлением. Сокращение количества звеньев ломаной, аппроксимирующей обрабатываемый контур, означало уменьшение объема управляющей программы.
Самый простой вариант решения поставленной задачи был очевиден: используя ЭВМ, можно было построить программу, которая постепенно увеличивала длину очередного шага до тех пор, пока стрелка прогиба обеспечивала допустимую точность ε. Однако идея тупого перебора казалась мало привлекательной – хотелось использовать более качественные математические методы, позволяющие за один шаг построить звено ломаной почти оптимальной длины. В такой постановке задача становилась вариационной, т.к. границы смежных звеньев оказывались переменными. Её удалось сначала решить для кривых с монотонно меняющейся кривизной при малых значениях допустимой точности ε отклонения звеньев ломаной. Идея решения напоминала метод малого параметра, используемый при решении задач устойчивости динамических систем. Величина стрелки прогиба в точке, максимально удаленной от звена ломаной, разлагалась в ряд. В силу малости отбрасывались члены ряда с более высокими степенями ε, а затем находились корни уравнения сначала второй степени. Потом аналогичная процедура повторялась для полинома третьей степени, в котором коэффициент при ε3 заменялся соответствующим квадратичным полиномом Чебышева, наименее, уклоняющимся от нуля.
Так были получены формулы для квазиоптимального шага, которые численно проверялись на различных кривых. Для одного и того же фрагмента кривой определялось количество N1 звеньев ломаной, построенных в сторону уменьшения кривизны, и количество N2 звеньев, построенных в обратном направлении. На довольно протяженном участке исходной кривой разность N1-N2 редко превышала 1. Аппроксимация в направлении уменьшения кривизны всегда приводила к звеньям, которые уклонялись от исходной прямой меньше, чем на ε. А в обратном направлении все звенья отклонялись чуть больше, чем на ε. Таким образом можно было установить верхнюю и нижнюю оценки для числа звеньев оптимальной ломаной. Более подробные результаты этого исследования и формулы для вычисления длины шага можно найти в работе [8]. Несколько позже аналогичное исследование было выполнено для кривых 2-го порядка с произвольным значением ε. Его результаты опубликованы в работе [9].
Чтобы оценить результаты проведенных исследований, приведу заключительную фразу из автореферата диссертации [10], защищенной в 1966 году: «Дальнейшее совершенствование аналитических способов задания криволинейных поверхностей выдвигает ряд новых математических проблем. Одной из них, в частности, является задача кусочно-полиномиальной аппроксимации плоских кривых и поверхностей». Таким образом, в этой работе была практически решена задача построения оптимальных сплайнов первого порядка и поставлена задача построения оптимального набора сплайнов более высокого порядка. В отечественной литературе это была первая работа в области сплайн-аппроксимации. Да из рубежом первые публикации по сплайнам появились пару лет спустя. Наиболее полная библиография первых зарубежных публикаций, приведенная в книге А.Фокса и М. Пратта «Вычислительная геометрия», ссылается на одну работу 1967 года (Гревилл), две работы 1968 года (Безье и Ауджа) и одну работу 1969 года (Гордон).
Список литературы
- Todd J. Communications on Pure and Applied Mathematic, v.8, № 1, 1955 (русский перевод: Дж. Тодд. Мотивы для работы в области численного анализа // «Математическое просвещение», вып.1, 1957)
- Motzkin T.S. Evaluation of the Polinomials. «Bull. Amer. Math. Society», 1955, v. 61, №2, p.163
- Кетков Ю.Л. Об одном способе вычисления полиномов на математических машинах. // Известия ВУЗ'ов. Радиофизика, т.1., № 4, 1958
- Люстерник Л.А., Червонскис О.А., Ямпольский А.Р. Математический анализ. Вычисление элементарных функций. М.: Гос. изд. физ. мат. литературы, 1963
- Кетков Ю.Л. Монография по спецтематике. Ростов-на-Дону, НИИТМ, 1964, 98 с.
- Шура-Бура М.Р. Система интерпретации ИС-2 // Сб. «Библиотека стандартных программ», Изд-во ЦБТИ, М., 1961
- Кетков Ю.Л. Автоматизация проектирования поверхностей корпусов судов при помощи ЭВМ. // В сб. Автоматизация технологического проектирования при помощи электронных вычислительных машин. М.: Машиностроение, 1966. – с.55-72
- Кетков Ю.Л. Об оптимальных методах кусочно-линейной аппроксимации. // Известия ВУЗов. Радиофизика, т.9, №6, 1966
- Кетков Ю.Л. О приближенных методах кусочно-линейной аппроксимации плоских кривых. // Ученые записки. Прикладная математика и кибернетика. Материалы к Всесоюзному межвузовскому симпозиуму по прикладной математике и кибернетике. Горький, 1967, с. 202-211
- Кетков Ю.Л. Об оптимальных методах аппроксимации плоских кривых и системе автоматизации программирования для обработки геометрической информации. // Автореферат диссертации на соискание ученой степени кандидата физико-математических наук. Горький, 1966
Об авторе: Нижегородский государственный университет им. Н.И. Лобачевского
Нижний Новгород, Россия
Материалы международной конференции Sorucom 2014 (13-17 октября 2014)
Помещена в музей с разрешения авторов
14 марта 2015
