К 80-летию Н. Вирта: Синтаксические диаграммы Н. Вирта в SYNTAX-технологии
Борис Константинович Мартыненко
Введение
Среди календарных дат 2014 года есть одна, связанная с 80-летием Никлауса Вирта, автора языка программирования Паскаль [1], широко используемого в мире и России для обучения программированию в старших классах школы и на первых курсах вузов. Вирт ввёл понятие синтаксических диаграмм, которое он использовал для наглядного представления структуры конструкций языка Паскаль. Впоследствии это понятие, родственное понятию графа, поручило дальнейшие развитие и применение в качестве средства реализации систем обработки данных, управляемых синтаксисом языков.
Использование графов [1] в математике началось ещё задолго до появления компьютеров. А когда они появились в 50-х годах прошлого века, и программирование велось в кодах вычислительной машины в условных адресах, то программисты часто применяли блок-схемы для документирования управляющей структуры машинных программ. Вскоре это привело к появлению теории схем программ [2].
Плодотворно ставятся на графах и другие задачи программирования: оптимальное распределение памяти, исследование потока данных в программах, эквивалентные преобразования КС-грамматик, автоматическая генерация тестов, семантические сети Г.С. Цейтина [3] в задачах искусственного интеллекта и т. д.
1. Проект реализации Алгола 68
В начале 1970-х группа сотрудников Вычислительного центра и лаборатории математической лингвистики Ленинградского государственного университета под научным руководством Г. С. Цейтина приступила к изучению языка программирования Алгол 68 [4] и, вскоре, к его реализации на ЕС ЭВМ [3] по заказу Научноисследовательского центра электронной вычислительной техники (НИЦЭВТ) Министерства радиоэлектронной промышленности СССР (отчёт об этом проекте см. в [5]).
Язык Алгол 68 в то время ещё не был «заморожен»: поправки поступали в каждом номере Алгол-Бюллетеня, некоторые выпуски которого содержали вложения – микрофиши с описанием синтаксиса этого языка в виде синтаксических диаграмм Н. Вирта. Это привело к идее использовать синтаксические диаграммы Вирта, как основы, для внутреннего представления структуры предложений входного языка в системе его реализации.
Синтаксис Алгола 68 определяется двухуровневыми грамматиками А. ван Вейнгаардена, порождающими рекурсивно-перечислимые множества, задача распознавания которых в общем случае алгоритмически не разрешима. На эффективные анализаторы, использующие непосредственно грамматики этого класса, рассчитывать не приходилось. Исходную грамматику можно было рассматривать лишь как первоначальную форму спецификации синтаксиса языка, то есть только как документ. Требовалось найти эффективный метод анализа языка Алгол 68 на основе других, более простых, классов грамматик, и построить адекватный инструмент, его реализующий. Позднее он был воплощён в технологическом комплексе (ТК) SYNTAX [6].
2. Трансляционные RBNF-грамматики
Трансляционная грамматика есть формальная система Gt = (Gc , E) , где Gc – управляющая грамматика; E – описание операционной среды.
2.1. Управляющая RBNF-грамматика есть шестёрка Gc = (N, T, ℜ, Σ, P, S), где N – словарь нетерминалов, T – словарь терминалов, ℜ – словарь резольверных символов (резольверов), Σ – словарь семантических символов (семантик), P={A: RA.| A∈N, RA – регулярное выражение относительно символов из множества N⋃T⋃ℜ⋃Σ} – множество правил, S – начальный нетерминал.
Управляющая грамматика специфицирует синтаксическое управление – множество цепочек C(Gc) = λ(RS) над терминальными и контекстными символами (т. е. символами из множества T⋃ℜ⋃Σ, где λ(R) определяется в зависимости от вида R следующим образом:
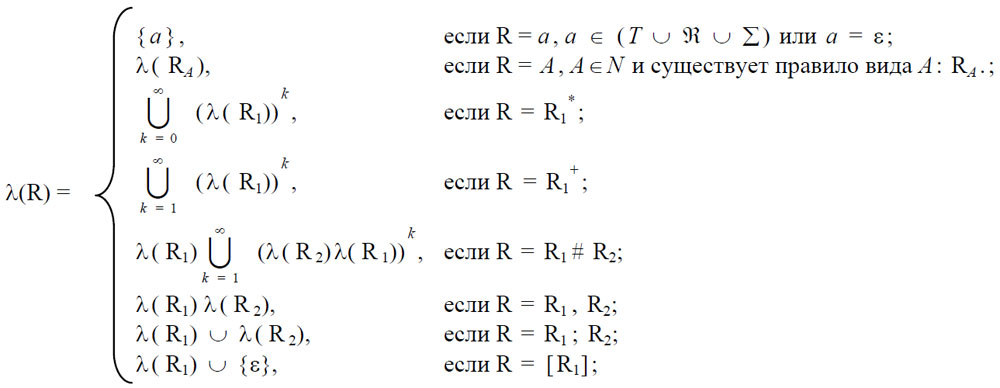
Здесь R1 и R2 – некоторые регулярные выражения. Определение вида регулярного выражения производится с учётом старшинства операций и расстановки скобок. Предполагается, что наивысшее старшинство имеют унарные операции *и + -Клини, затем бинарные операции: итерация с разделителем (#), далее конкатенация (,) и, наконец, объединение (;).
2.2. Описание операционной среды. Описанием операционной среды называется формальная система E = (E, H, Iℜ ,IΣ, e0) , где E – пространство состояний операционной среды – область определения предикатов: Iℜ ={ιρ: E→{false, true}| ρ∈ℜ}, ассоциированных с резольверными символами, и преобразований операционной среды: IΣ ={ισ: E→E | σ∈Σ}, ассоциированных с семантическими символами; H – объектное подпространство, то есть та часть операционной среды, состояние которой представляет особый интерес [4]; e0∈E – начальное состояние операционной среды.
3. Трансляция, определяемая трансляционной грамматикой
Пусть e∈E – некоторое состояние операционной среды, ρ∈ℜ* – некоторая резольверная цепочка, а σ∈Σ* – некоторая семантическая цепочка.
Положим по определению
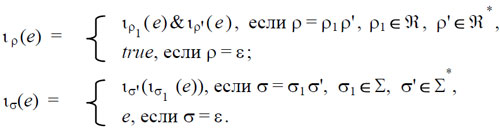
Здесь ιρ1 и ισ1 определяются описанием операционной среды, а ιρ' и ισ' – рекурсивные ссылки на соответствующие определения, приведённые выше.
Трансляционная грамматика определяет трансляцию: τ(Gt) = {(x, [e]H) | ∃cx(cx∈C(Gc), cx = κ0α1κ1α2 … κm-1αmκm – управляющая цепочка; κi∈(ℜ⋃Σ)* (i = 0, 1, 2, ... , m) – цепочки контекстных символов, в которых ρi∈ℜ* – резольверные подцепочки, σi∈Σ*– семантические подцепочки; aj∈T(j = 1, 2,..., m) – терминальные символы; x = α1α2… αm– входная цепочка (предложение входно го языка); e = ισm (...ισ1(e0)) – финальное состояние операционной среды при условии, что ισ0(e0) & ισ1(e1) & ... & ισm(em) = true, где en+1= ισn(en) (n = 0, 1, ... , m); очевидно, что e = em+1)}. Здесь [e]H обозначает проекцию точки e∈E на объектное подпространство H – результат трансляции входной цепочки x.
Другими словами, трансляция есть множество пар, в которых первая компонента есть предложение входного языка, а вторая – проекция состояния операционной среды после её преобразований посредством семантик, входящих в соответствующую управляющую цепочку. Заметим, что управляющая цепочка и вместе с ней предложение входного языка определяются с учётом контекстных условий, задаваемых резольверами. При этом предполагается, что резольверы вычисляются синхронно с семантическими преобразова-ниями по порядку вхождений контекстных символов в управляющую цепочку. Синхронизация означает, что сначала вычисляются предикаты, ассоциированные с резольверными символами, предшествующими терминалу α1, в порядке их следования. Если все они выполняются, то исполняются преобразования операционной среды, ассоциированные с семантическими символами, предшествующими терминалу α1 (также в текстуальном порядке). Затем аналогичным порядком выполняются резольверы и семантики, предшествующие терминалу α2, и т. д. Процесс заканчивается, когда успешно завершается вычисление конъюнкции предикатов, следующих за символом am, и исполнение соответствующих семантик.
Синтаксически правильными считаются лишь те входные цепочки, которые входят в состав управляющих цепочек, на которых выполняются все предикаты, ассоциированные с их резольверными символами. «Смысл» входного предложения x представляется семантической цепочкой σ1σ2…σn.
Если некоторому входному предложению соответствует несколько управляющих цепочек с разными семантическими составляющими, то такое предложение называется семантически неоднозначным. В SYNTAX-технологии семантическая неоднозначность не допускается [5]. Однако использование резольверов во многих случаях помогает избегать этой опасности. В ТК SYNTAX управляющие грамматики записываются на языке TSL [6]. Именно по ним генерируются граф-схемы. Операционная среда описывается на языке программирования Borland Pascal 7.0 и после компиляции представляется виде DLL-библиотеки.
Приведём пример трансляционной грамматики, иллюстрирующий спецификацию интерпретатора арифметических выражений (калькулятора).

CALC – трансляционная грамматика калькулятора
Поясним, что спецификация трансляционной грамматики состоит из трёх разделов. Раздел MICROLEXICS содержит информацию для построения транслитератора.
Задача последнего – распределить символы входного алфавита по лексическим классам. Именно лексические классы, а не сами символы, управляют процессом обработки входного текста на стадии синтаксиса, описываемого в разделе SYNTAX.
Из словаря нетерминалов выделяются вспомогательные понятия (Auxiliary notions), если они определяются прямо или косвенно регулярными выражениями. Они вставляются в граф-схему механизмом макроподстановок.
Пример граф-схемы, построенной по управляющей грамматике калькулятора до раскрытия вспомогательных понятий [7], показан на рис. 1 в разд. 4. Как видно на рисунке, дуги граф-схем помечены контекстными символами, в то время как дуги синтаксических диаграмм Вирта никак не помечаются.
Разделы ENVIRONMENT и IMPLEMENTATION, описывающие окружение и интерпретацию контекстных символов в этом окружении, здесь не показаны. Они преобразуются в DLL-библиотеку посредством транслятора на той платформе, на которой реализуется инструментальный комплекс SYNTAX-технологии.
4. Спецификация трансляций при помощи трансляционных граф-схем
В SYNTAX-технологии используется три различных формы спецификации трансляций, одна из которых (RBNF-грамматика) удобна для первоначального задания трансляций, другая (процессор) является формой реализации трансляций, а третья (трансляционная граф-схема) есть промежуточная форма между двумя первыми. Эта форма, аналогичная синтаксическим диаграммам Вирта, может использоваться для описания синтаксиса языков и спецификации трансляций непосредственно, тем более что граф-схемы являются более гибким аппаратом для задания трансляций, чем грамматики [8]. В технологическом комплексе SYNTAX она применяется также при автоматической генерации прототестов.
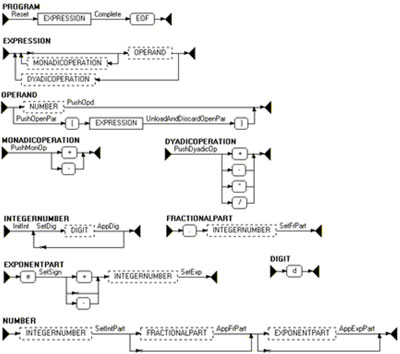
Рис. 1. Представление управляющей граф-схемы, построенной по грамматике CALC, до раскрытия вспомогательных понятий
Трансляционная граф-схема G = (Gc, E), как и трансляционная грамматика, состоит из двух компонент: управляющей граф-схемы (Gc) и описания операционной среды (E).
Управляющая граф-схема является графовым аналогом управляющей грамматики. Каждое правило RBNFграмматики представляется в виде отдельного связного ориентированного графа, вершины которого помечены терминалами или нетерминалами грамматики, а дуги – цепочками, составленными из резольверных и семантических символов, с возможными петлями, циклами и параллельными дугами (так что уместнее было бы говорить о псевдомультиграфе).
Такой граф имеет две особые вершины: начальную и конечную. Особенность этих вершин в том, что в начальную вершину ни одна дуга не входит, а из конечной вершины ни одна дуга не выходит. Все другие, внутренние вершины, помечены терминальными или нетерминальными символами. В частности, дуги могут помечаться пустыми цепочками, и тогда они называются непомеченными. Если все дуги управляющей граф-схемы не помечены, то она называется синтаксической граф-схемой. Последнее, как уже отмечалось, есть не что иное, как синтаксические диаграммы Вирта.
Таким образом, в общем случае управляющая граф-схема – это несвязный помеченный граф, в котором одна компонента связности представляет одно правило управляющей грамматики. Очевидно, что управляющая граф-схема, как формальная система, вполне аналогична управляющей грамматике с той лишь разницей, что правила имеют графовую форму, т. е. Gc = (N, T, ℜ, Σ, K,S), где N – нетерминалы, T – терминалы, ℜ – резольверы, Σ – семантики, K={KA │A∈N, KA – компонента графа, определяющая нетерминал A}, S∈N – начальный нетерминал.
Компоненту KS, определяющую начальный нетерминал S, назовем заглавной компонентой управляющей граф-схемы.
Описание операционной среды (E) наследуется от трансляционной грамматики.
Как и управляющая грамматика, управляющая граф-схема порождает синтаксическое управление. Порождение управляющих цепочек реализуется с помощью порождающих маршрутов следующим образом. Назовем маршрут в некоторой компоненте управляющей граф-схемы полным, если он начинается в начальной и заканчивается в конечной вершине этой компоненты. Следом маршрута назовем последовательность меток вершин и дуг, составляющих этот маршрут.
Рассмотрим некоторый полный маршрут в заглавной компоненте управляющей граф-схемы и определим его след. Каждое вхождение нетерминала в следе заменим на след некоторого полного маршрута в компоненте граф-схемы, определяющей этот нетерминал. Цепочку, получаемую в результате многократного повторения таких подстановок и не содержащую ни одного вхождения нетерминала, назовем структурированной управляющей цепочкой. Начальные и конечные метки придают ей структуру, соотносящую отдельные её фрагменты с компонентами, их породившими.
Структурированная управляющая цепочка является аналогом скобочного представления дерева вывода в КС-грамматике. Обычная управляющая цепочка получается из структурированной, если в ней игнорировать начальные и конечные маркеры.
Отметим, что компоненты используются лишь после того, как в них раскрыты все вспомогательные понятия.
Фактически используется линейное представление «раскрытых» диаграмм в виде массива записей из двух полей: тип записи и информационное поле, соответствующее этому типу.


Машинное (линейное) представление графа есть последовательность занумерованных записей. Такая запись состоит из двух полей, одно из которых определяет её тип, а другое – информационное. Записи типа "begin" и "end" представляют начальную и конечную вершину соответственно. Их информационные поля содержат определяемый данной компонентой нетерминальный символ.
Записи типа T и N представляют терминальные и нетерминальные вершины, а их информационные поля содержат символы из соответствующих словарей. Типы записей FR, BR, FS и BS – представляют соответственно резольверы и семантики прямого и обратного просмотров. Записи типа "разветвление" (–<) и "переход" (→), в которых информационные поля представлены номерами других записей, определяют возможный порядок обхода компонент управляющей граф-схемы.
5. Челночный сплайновый процессор
Челночным сплайновым процессором назовем формальную систему Ps =(Pcf, Pcb, E), состоящую из управляющего сплайнового процессора прямого просмотра Pcf, управляющего сплайнового процессора обратного просмотра Pcb и операционной среды E, компилируемой по её описанию E.
5.1. Прямой просмотр. Управляющим процессором прямого просмотра назовем формальную систему Pcf = (Qf, Σf, Гf, ∆f, ℜf, δf, q0f, Ff ), в которой Qf – множество состояний управления прямого просмотра; Σf – входной алфавит прямого просмотра; Гf – алфавит магазинных символов прямого просмотра; ∆f – алфавит семантических символов прямого просмотра; ℜf – алфавит резольверных символов прямого просмотра; δf = (δ1f, δ2f, δ3f) – управляющая таблица прямого просмотра, состоящая из таблицы резольверов прямого просмотра δ1f: Qf × (Σf ⋃ {ε}) →2ℜf*, таблицы управляющих элементов прямого просмотра δ2f: Qf × (Σf ⋃ {ε}) × ℜf* → (Qf ⋃ {Sup}) × Гf* × ∆f*, и таблицы возвратных состояний δ3f: Qf × Гf × ℜf* → Qf; q0f – начальное состояние прямого просмотра; Ff ⊆ Qf – множество конечных состояний прямого просмотра.
5.2.Обратный просмотр. Управляющим процессором обратного просмотра назовем формальную систему Pcb = (Qb, Σb, Гb, ∆b, ℜb, δb, q0b, Fb ), в которой Qb – множество состояний управления обратного просмотра; Σb – входной алфавит обратного просмотра; Гb – алфавит магазинных символов обратного просмотра; ∆b – алфавит семантических символов обратного просмотра; ℜb – алфавит резольверных символов обратного просмотра; δb = (δ1b, δ2b) – управляющая таблица обратного просмотра, в которой δ1b: Qb × (Σb ⋃ {ε}) →2ℜb* – таблица резольверов обратного просмотра, а δ2b: Qb × (Σb ⋃ {ε}) × ℜb* → (Qb ⋃ {Pop}) × (Гb ⋃ {ε}) × ∆b* – таблица управляющих элемен-тов обратного просмотра; q0b – начальное состояние обратного просмотра; Fb ⊆ Qb – множество конечных состояний обратного просмотра.
5.3.Операционная среда. Понятие операционной среды, включающей интерпретацию контекстных (т. е. резольверных и семантических резольверных) символов, определённое для трансляционных грамматик, используется в сплайновых процессорах с учётом того, что ℜ = ℜf ⋃ ℜb, ℜf ⋂ ℜb = ∅, ∆ = ∆f ⋃ ∆b, ∆f ⋂ ∆b = ∅ [9], и что контекстные символы из ℜf и ∆f интерпретируются на прямом просмотре, а резольверы и семантики из ℜb и Σb – на обратном.
6. Функционирование челночного сплайнового процессора
Работу челночного сплайнового процессора опишем в терминах его конфигураций.
6.1. Прямой просмотр действует с начальной конфигурации (q0f, x, ε, e0f), где q0f ∈ Qf – начальное состояние его управления; x ∈ Σf* – входная цепочка; ε означает, что первоначально магазин пуст; e0f – начальное состояние операционной среды.
Пусть (q1f, ax, α, e1f) – текущая конфигурация прямого просмотра, в которой q1f ∈ Qf – текущее состояние его управления; ax ∈ Σf* – необработанная часть входной цепочки, где a ∈ Σf – текущий входной символ, x ∈ Σf* – остаток входной цепочки; α ∈ Гf* – текущая магазинная цепочка, причём считается, что на вершине магазина находится крайний левый символ цепочки α; e1f – текущее состояние операционной среды. Очередное движение определяется управляющей таблицей прямого δf.
Случай 1. δ1f(q1f, a) ≠ ∅ – существуют контексты приёма входного символа a.
Случай 1.1. ∀(ρ ∈ δ1f(q1f, a)) : (~ιρ(e1f)).
– Диагностируется контекстная ошибка по входному символу a.
Случай 1.2. ∃(ρ, ρ'∈ δ1f(q1f, a)): ((ρ ≠ ρ') & (ρ ≠ ε) & (ρ' ≠ ε) & ιρ(e1f) & ιρ'(e1f).
– Диагностируется контекстная неоднозначность по входному символу a.
Случай 1.3. (δ1f(q1f, a)) = {ρ}) & (ρ ∈ ℜf*) & ιρ(e1f) – приём a.
Пусть δ2f(q1f, a, ρ) = (q2f, γ, σ), где q2f ∈Qf – переходное состояние, γ ∈ Гf* – магазинная цепочка, σ ∈ ∆f* – семантическая цепочка. Тогда (q1f, ax, αX, e1f) 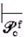 (q2f, x, γXα, e2f).
(q2f, x, γXα, e2f).
После этого новая конфигурация анализируется сначала.
Случай 2. δ1f(q1f, a) = ∅ – не существуют контексты приёма a.
Случай 2.1. δ1f(q1f, ε) ≠ ∅ – существуют контексты приёма ε.
Случай 2.2.1. ∀(ρ ∈ δ1f(q1f, ε)) : (~ιρ(e1f)).
– Диагностируется контекстная ошибка по ε -движениям.
Случай 2.2.2. ∃(ρ, ρ'∈ δ1f(q1f, ε)): ((ρ ≠ ρ') & (ρ ≠ ε) & (ρ' ≠ ε) & ιρ(e1f) & ιρ'(e1f).
– Диагностируется контекстная неоднозначность выбора ε-движения.
Случай 2.2.3. (δ1f(q1f, ε)) = {ρ}) & (ρ ∈ ℜf*) & ιρ(e1f)
Движение процессора однозначно определяется управляющим элементом δ2f(q1f, ε, ρ).
Пусть δ2f(q1f, ε, ρ) = (Sup [10], γ, σ), где γ ∈ Гf*, σ ∈ ∆f*. Процессор выполняет переход вида (q1f, ax, αX, e1f) 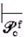 (q1f, ax, γXα, e2f). Здесь e2f = ιρ(e1f).
(q1f, ax, γXα, e2f). Здесь e2f = ιρ(e1f).
Пусть γXα = Zβ, где Z ∈ Гf, β ∈ Гf*. Тогда фактически (q1f, ax, γXα, e2f) = (q1f, ax, Zβ, e2f). Если при этом δ3f(q1f, Z, ρ) = q2f, то процессор совершает ещё один шаг перехода вида (q1f, ax, Zβ, e2f) 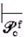 (q2f, ax, β, e2f).
(q2f, ax, β, e2f).
Новое состояние q2f называется возвратным, а исходное – подавляемым. Далее анализ новой конфигурации начинается с начала при том же текущем входном символе.
Прямой просмотр заканчивает свою работу тогда, когда он достигает одного из своих конечных состояний при пустом магазине. Вся последовательность движений прямого про-смотра может быть представлена следующим образом: (q0f, x, ε, e0f)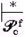 (pf, ε, ε, ef), где pf ∈ Ff. Достигнутое состояние операционной среды ef является начальным для обратного просмотра. Подразумевается, что вся последовательность состояний управления прямого просмотра регистрируется на его выходе и передаётся на вход обратного просмотра.
(pf, ε, ε, ef), где pf ∈ Ff. Достигнутое состояние операционной среды ef является начальным для обратного просмотра. Подразумевается, что вся последовательность состояний управления прямого просмотра регистрируется на его выходе и передаётся на вход обратного просмотра.
6.2. Обратный просмотр, сканируя в обратном порядке последовательность состояний управления прямого просмотра, продолжает изменение состояний операционной среды, начиная со своей начальной конфигурации, которая имеет вид (q0b, pf ... q0f, ε, ef).
Пусть (q1b, qkfqk–1f… q0f, α, e1b) – текущая конфигурация обратного просмотра. Очередное движение обратного просмотра определяется его управляющей таблицей δb в зависимости от ситуации.
Случай 1. δ1b(q1b, qkf) ≠ ∅ – существуют контексты приёма qkf.
Случай 1.1. ∀(ρ ∈ δ1b(q1b, qkf)) : (~ιρ(e1b)).– Диагностируется контекстная ошибка по состоянию прямого просмотра qkf.
Случай 1.2. ∃(ρ, ρ'∈ δ1b(q1b, qkf)): ((ρ ≠ ρ') & (ρ ≠ ε) & (ρ' ≠ ε) & ιρ(e1b) & ιρ'(e1b).
– Диагностируется контекстная неоднозначность по состоянию прямого просмотра qkf.
Случай 1.3. (δ1b(q1b, qkf)) = {ρ}) & (ρ ∈ ℜb*) & ιρ(e1b).
Пусть δ2b(q1b, qkf, ρ) = (q2b, γ, σ), где q2b ∈ Qb – переходное состояние, γ ∈ (Гb ⋃ {ε}) – магазинная цепочка[11], σ ∈ ∆b* – семантическая цепочка. В терминах конфигураций имеем: (q1b, qkfqk–1f… q0f, α, e1b) 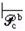 (e2b, qk–1f… q0f, γα , e2b).
(e2b, qk–1f… q0f, γα , e2b).
После этого новая конфигурация анализируется сначала.
Случай 2. δ1b(q1b, qkf) = ∅ – не существуют контексты приёма qkf.
Случай 2.1. δ1b(q1b, ε) ≠ ∅ – существуют контексты приёма ε.
Случай 2.2.1. ∀(ρ ∈ δ1b(q1b, ε)) : (~ιρ(e1b))
– Диагностируется контекстная ошибка по ε.
Случай 2.2.2. ∃(ρ, ρ') ∈ δ1b(q1b, ε): ((ρ ≠ ρ') & (ρ ≠ ε) & (ρ' ≠ ε) & ιρ(q1b) & ιρ'(e1b).
– Диагностируется контекстная неоднозначность выбора ε-движения.
Случай 2.2.3. (δ1b(q1b, ε)) = {ρ}) & (ρ ∈ ℜb*) & ιρ(e1b).
Пусть (δ2b(q1b, ε, ρ)) = (Pop[12], γ, σ), где γ ∈ (Гb ⋃ {ε}), σ ∈ ∆b*. В этом случае выполняется переход вида (q1b, qkfqk–1f… q0f, α, e1b) 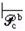 (q1b, qk–1f… q0f, γα , e2b), где e2b = ισ(e1b).
(q1b, qk–1f… q0f, γα , e2b), где e2b = ισ(e1b).
Пусть магазинная цепочка, образовавшаяся после записи γ над верхним символом магазина, есть γα = Xβ. Тогда имеем (q1b, qk–1f… q0f, γα , e2b) = (q1b, qk–1f… q0f, Xβ, e2b).
Далее процессор совершает ещё один шаг перехода, а именно: (q1b, qk–1f… q0f, Xβ, e2b) 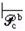 (q2b, qk–1f… q0f, β, e2b), где q2b = X.
(q2b, qk–1f… q0f, β, e2b), где q2b = X.
Это последнее движение затрачивает верхний символ магазина, но текущий входной символ всё ещё остаётся не принятым. Новое состояние q2b называется возвратным, а исходное q1b – подавляемым.
Далее разбор новой конфигурации начинается по той же схеме и при том же текущем входном символе.
Вся последовательность движений обратного просмотра может быть представлена следующим образом: (q0b, pf ... q2f, ε, ef) 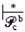 (pb, ε, ε, eb). Здесь pb ∈ Fb – конечное состояние обратного просмотра, прочитана вся последовательность состояний прямого просмотра и магазин пуст.
(pb, ε, ε, eb). Здесь pb ∈ Fb – конечное состояние обратного просмотра, прочитана вся последовательность состояний прямого просмотра и магазин пуст.
Итак, трансляцией, реализуемой челночным сплайновым процессором, которую мы также будем называть челночной трансляцией, называется множество пар:
τ(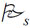 )={(x, [eb]H) | (q0f, x, ε, e0f)
)={(x, [eb]H) | (q0f, x, ε, e0f) 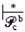 (pf, ε, ε, ef), pf ∈ Ff, (q0b, pf ... q0f, ε, ef)
(pf, ε, ε, ef), pf ∈ Ff, (q0b, pf ... q0f, ε, ef) 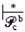 (pf, ε, ε, eb), pb ∈ Fb}.
(pf, ε, ε, eb), pb ∈ Fb}.
Заключение
Известно [7], что структура любого предложения КС-языка может быть представлена в виде дерева вывода, отображающего его на правила грамматики. В описываемом методе используется другая постановка задачи синтаксического анализа: по данному предложению КС-языка выделить из леса деревьев, порождающих язык, то дерево, результат которого равен этому предложению.
Описанный здесь метод трансляции использует RBNF-грамматики, подобные КС-грамматикам, правила которых определяют терминальные порождения через регулярные выражения относительно символов алфавитов грамматики и, вновь введённых, контекстных символов – семантик и резольверов (предикатов). С каждым семантическим символом ассоциируется некоторое преобразование операционной среды – пространства данных, составляющих контекст, а с каждым из резольверных символов – предикат, заданный в том же пространстве. Такая грамматика порождает язык, аппроксимируемый регулярными сплайнами.
Внутренней задачей транслятора является реконструкция управляющей цепочки по предложению входного языка и её интерпретация. Эта реконструкция равносильна нахождению в управляющей граф-схеме маршрутов, порождающих данное предложение входного языка. Задача нахождения порождающего маршрута решается в два просмотра, один из которых – прямой сканирует входную цепочку в прямом направлении, а другой – обратный сканирует последовательность состояний конечного управления прямого просмотра в качестве своей входной цепочки. Каждый из этих просмотров использует магазин[13]. Естественно, контекстные символы относятся к соответствующим просмотрам. Собственно трансляция осуществляется семантическими процедурами при учёте контекста предикатами, интерпретирующими резольверные символы.
Построение и оптимизация челночного сплайнового процессора, описанного в разделе 6, производится по управляющей грамматике, представленной в виде граф-схемы с ограничениями, гарантирующими его детерминизм. Эти ограничения формулируются в терминах граф-схемы и учитываются во время его построения [6]. Соответствующий языковой процессор подобен множеству конечных автоматов, каждый из которых распознает свой фрагмент входной цепочки – регулярный сплайн, и обрабатывает его с учётом состояния контекста. Класс языков, определяемых RBNF-граф-схемами через порождающие маршруты, есть LL(1) и, следовательно, имеют линейную оценку сложности по времени относительно длины входного предложения [7].
Список литературы
1. Wirth, N. The Programming Language Pascal. Acta Informatica, Vol. 1, 1971, pp. 3563.
2. Янов Ю. И. О логических схемах алгоритмов // Проблемы кибернетики – 1958. Вып. 1. С. 75-127.
3. Цейтин, Г. С. Программирование посредством ассоциативных сетей. В: ЭВМ в проектировании и производстве, вып. 2 / (Г. В. Орловский, ред.), "Машиностроение", Л, 1985, С. 16-48.
4. Пересмотренное сообщение об Алголе 68. / Ред. А. Ван Вейнгаарден, Б. Майу, Дж. Пек, К. Костер, М. Синцов, Ч. Линдси, Л. Меертенс, Р. Фискер. М.: "Мир", 1979. 534 с.
5. Алгол 68. Методы реализации / Под ред. Г.С. Цейтина. Л.: Изд-во Ленингр. ун-та, 1976. 224 с.
6. Б. К. Мартыненко. Синтаксически управляемая обработка данных. – Санкт-Петербург: Изд-во С.-ПбГУ, 2004. – 316 с.
7. Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. Т.1. Синтаксический анализ, 612 с.; Т.2. Компиляция, 487 с., М.: Мир, 1978.
Примечания.
1. Отцом теории графов (так же как и топологии) является Эйлер (1707–1782), решивший в 1736 г. широко известную в то время задачу, называвшуюся проблемой кёнигсбергских мостов.
2. Схемы Янова – схемы программ, которые были введены в литературу А.А. Ляпуновым и Ю.И. Яновым в 1958 г. и направлены на разработку общей теории условий, управляющих последовательностью выполнений операторов в программе.
3. Советский аналог серии System/360 и System/370 фирмы IBM, выпускавшихся в США с 1964 г.
4. Например, выходной файл.
5. Фактически семантическая неоднозначность контролируется при построении управляющих таблиц процессоров.
6. Описание языка TSL дано в [5, гл. 8].
7. На рис. 1 они показаны в пунктирных рамках.
8. Действительно, существуют граф-схемы, для которых невозможно построить прообраз управляющей грамматики, преобразование которого в граф-схему давало бы оригинальную граф-схему.
9. В трансляционных грамматиках для обозначения семантических символов вместо символа ∆ используется символ Σ, причём предполагается, что Σ = Σf ⋃ Σb и Σf ⋂ Σb = ∅.
10. Для ε-движения вместо переходного состояния всегда даётся специальное значение Sup (Suppress), означающее, что следующее (возвратное) состояние надо определять по таблице δ3f.
11. Для ε-движения вместо переходного состояния всегда даётся специальное значение Pop. Следующее (возвратное) состояние следует брать с вершины магазина.
12. Для ε-движения вместо переходного состояния всегда даётся специальное значение Pop. Следующее (возвратное) состояние следует брать с вершины магазина.
13.Если граф-схема не однокомпонентная.
Об авторе: Санкт-Петербургский государственный университет
Санкт-Петербург, Россия
mbk@ctinet.ru
Материалы международной конференции Sorucom 2014 (13-17 октября 2014)
Помещена в музей с разрешения авторов
20 июля 2015
