Уравновешенная (симметричная) троичная система счисления и её использование в вычислительных устройствах в докомпьютерную и компьютерную эпоху
В.И. Тихвинский
Уравновешенная троичная система счисления обладает теми же свойствами, что и другие системы счисления (СС). СС позволяет записать число специальными знаками (цифрами). Число показывает количество подсчитанных единиц и состоит из разрядов. Разряд числа – такое условное разделение числа на единицы, когда определённое количество единиц разряда образует единицу старшего разряда, а единица разряда состоит из определённого количества единиц младшего разряда. Разряд числа имеет свой вес, вес разряда показатель того, во сколько раз единицы разряда больше или меньше единиц того разряда, с которого начинается счёт. Основание СС – это показатель того, во сколько раз единица разряда больше единицы предыдущего разряда. [1]
Уравновешенная троичная система счисления родилась из задачи “о взвешивании”. Эта задача была известна ещё Фибоначчи (ок. 1170—ок. 1250). В задаче требовалось найти наименьшее количество гирь для взвешивания на двухчашечных весах груза массой от 1 до 40 единиц, при этом гири можно было располагать на любой из чаш весов. Оказалось, что для решения такой задачи потребуются только четыре гири с весом 1, 3, 9, 27 единиц. Нетрудно заметить, что вес последующих гирь растёт точно так же, как растёт математический вес разрядов в троичной системе счисления, т. е. вес каждой последующей гири, как и вес каждого последующего разряда троичного числа, в три раза больше предыдущего веса. Т. к. гири располагаются на разных чашах весов, то их вес относительно взвешиваемого груза может иметь как положительное, так и отрицательное значение. Если мы хотим воспользоваться недостающей гирей весом в 2 единицы, то мы должны на чашу весов с грузом положить гирю с весом 1, а на противоположную с весом 3. Ясно, что это будет соответствовать весу гири в 2 единицы, т. к. вес гири 1 вычитается из веса гири 3 (см. рис.1). Таким образом, используя четыре гири, кладя их на различные чаши весов, можно получить любой вес от 1 до 40 единиц.

Рис. 1
Целое число в уравновешенной троичной системы счисления (УТСС) можно записать по формуле
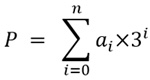
Рис. 1
, где:
P – значение, записанное в троичное число,
i – индекс текущего разряда числа,
n – индекс последнего разряда числа,
ai – разряд числа, ai є (-1; 0; 1),
3i – вес разряда числа.
Отличительной особенностью УТСС от других СС является то, что отдельного знака для всего числа не существует, но при этом каждый разряд числа имеет свой знак. Является ли число, записанное в УТСС, положительным или отрицательным, определяется по знаку в старшем разряде числа. Поменять знак числа на обратный значит поменять его во всех разрядах числа. [2]
Первым человеком, реализовавшим автоматический счёт в УТСС, был англичанин Томас Фаулер. К сожалению, его счётная машина не получила государственной финансовой поддержки, и, хотя была изготовлена и продемонстрирована в мае 1840 г. Чарлзу Бэббиджу, её чертежи не были опубликованы, и она была забыта. Финансирование ушло на построение машины Чарлза Бэббиджа, которая использовала десятичное основание для вычислений, что значительно усложняло и удорожало машину. [2, 3]
В августе 2000 г. в США, Марком Глускером была создана работающая механическая счётная машина для УТСС. Машина чисто демонстрационная, имеет три троичных разряда и воспроизводит то, как могла бы осуществляться операция умножение на машине Фаулера. Тем не менее, эту машину нельзя считать моделью машины Фаулера, т. к. сохранившиеся сведения о машине Фаулера весьма скудные, это скорее предположение о том, как могла бы быть устроена машина Фаулера. [2]

Рис. 2. Модель счётной машины Фаулера
Не вдаваясь в подробности воссозданной модели, позволим себе некоторое фантазирование и продемонстрируем насколько упрощается конструкция Счислителя Куллера (СК), если в нём использовать не десятичную СС, а УТСС. СК был подробно описан нами в [1].
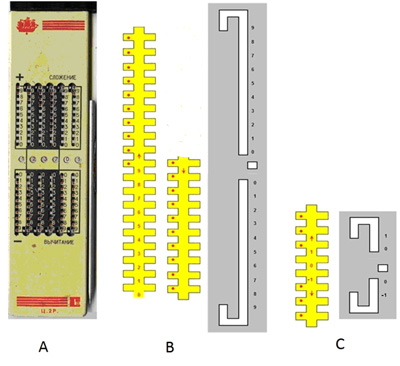
Рис. 3. А – СК в современном исполнении, В – фрагменты счётной рейки и маска для рейки СК, С - счётная рейка и маска для рейки СК для вычисления в УТСС
Мы видим, насколько сократилась длина счётной рейки в СК. Помимо этого, появилась возможность оперировать на СК не только положительными, но и отрицательными числами, причём при получении такого существенного преимущества принцип устройства СК не изменился.
Жаль, что УТСС была использована только в одном механическом счётном устройстве (МСУ) – в счётной машине Фаулера. МСУ было бы удешевлено при использовании УТСС по сравнению с устройством, использующим десятичную СС. Однако не всё так просто, как кажется на первый взгляд. При вычисление на МСУ для УТСС необходимо производить преобразования из десятичной СС в УТСС и обратно. В счётной машине Фаулера не было шифратора и дешифратора для рассмотренных выше преобразований, преобразования осуществлялись не автоматически, а посредством специально составленных для этого таблицы, что вызывало определённые неудобства. [2]
Электронный автоматический счёт на основе УТСС был реализован на советских ЭВМ “Сетунь” (в декабре 1958 г. построен опытный образец) и “Сетунь-70” (опытный образец был готов в апреле 1970 г.) Главным конструктором ЭВМ “Сетунь” являлся заслуженный научный сотрудник МГУ Николай Петрович Брусенцов. [3, 4].
Разряд троичного числа, представленный в памяти ЭВМ, назывался тритом, трит содержит в себе одно из трёх значений: -1, 0, 1, в отличие от бита, разряда двоичного числа, который содержит в себе одно из двух значений: 0, 1. Триты содержатся в трайтах, один трайт представляет собой троичное число, состоящее из шести трит, в отличие от байта, представляющего собой двоичное число, которое состоит из восьми бит. Несколько байтов или трайтов составляют компьютерное слово. При одной и той же точности представления цифр в двоичной СС (ДСС) и УТСС троичное слово получается короче двоичного в 1,6 раза, а скорость выполнения арифметических операций в 1,6 раза быстрее при использовании УТСС. [4] При использовании УТСС не требуется дополнительного знакового разряда и не требуется использования дополнительного кода для представления отрицательных чисел, в отличие от ДСС. В УТСС упрощается замена знака на противоположный по сравнению с ДСС, также упрощается операция округления числа, в УТСС она сводится к операции отбрасывания младших, незначащих разрядов. [2-4] В УТСС также сокращается количество шагов на операцию ветвления, так для определения, является ли число положительным, отрицательным или равным нулю, при использовании УТСС в ЭВМ понадобится только одно ветвление, а при использовании ДСС два (рис. 4) [3].
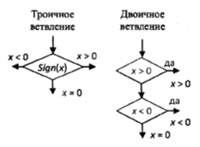
Рис.4. Троичное и двоичное ветвление
В настоящее время в ЭВМ широко используется ДСС, но правильно ли было использовать двоичное основание в электронных вычислительных устройствах? Ясно, что использование ДСС в вычислительных устройствах было прогрессом по сравнению с использованием десятичной СС, но досадно то, что на УТСС, имеющую явные преимущества перед ДСС, так мало обращали внимания изобретатели вычислительных устройств.
Список литературы
- Тихвинский В.И. Предыстория автоматизации вычислений в докомпьютерную эпоху, Менеджмент и Бизнес-Администрирование, №3, – М.: 2015, с. 199-202.
- Шилов В.В. Уравновешенная троичная система счисления и Томас Фаулер. http://www.computer-museum.ru/precomp/fauler.htm
- Владимирова Ю.С. Введение в троичную информатику, –М.: АРГАМАК-МЕДИА, 2015, 160 с.
- Страница истории отечественных ИТ, Том 1. –М.: ООО Альпина Паблишер 2015.
Об авторе: Тихвинский Виталий Игоревич,
старший преподаватель кафедры информатики,
Российский экономический университет имени Г.В. Плеханова,
E-mail: tvitaly1@yandex.ru.
Помещена в музей с разрешения автора
6 июня 2017
