Особенности программирования и математическое обслуживание для машины «Сетунь»
Е. А. Жоголев
1. Программирование на машине «Сетунь» [1, 2] имеет много своеобразных особенностей, заметно выделяющих ее из ряда цифровых автоматических машин. Помимо особенностей, связанных с наличием в машине фиксированной запятой и с одноадресной системой команд, весьма интересны приемы программирования, использующие особенности троичной системы счисления. Программирование на машинах с малой емкостью оперативной памяти (или с многоступенчатой ее структурой) относится к еще малоизученной области программирования. Трудности, которые при этом возникают, могут быть успешно преодолены частично за счет разработки специальных приемов программирования и особенно за счет использования средств автоматического программирования. Разрешению этих трудностей на машине «Сетунь» способствует наличие в ней сравнительного быстрого обмена информацией между оперативной памятью и магнитным барабаном, являющимся основным видом памяти на этой машине.
«Сетунь» является первой в Советском Союзе машиной с алфавитно-цифровыми устройствами ввода и вывода. Хотя назначение таких устройств общеизвестно и роль их как для окончательной обработки и оформления результатов, так и для автоматического программирования понятна для каждого, кто хотя бы раз этим воспользовался, все же эффективное их использование связано с ломкой некоторых старых традиций и разработкой новых приемов программирования.
В данной статье дается обзор основных приемов программирования и системы математического обслуживания, используемых на машине «Сетунь». При этом мы не будем здесь касаться ряда вопросов использования режима фиксированной запятой и особенностей программирования на одноадресных машинах, достаточно полно изложенных в литературе [3, 4, 5, 6].
2. Троичная система счисления с цифрами -1, 0, 1 обладает двумя весьма полезными свойствами.
Свойство 1. Наилучшее округление числа x до k верных троичных знаков получается отбрасыванием всех младших знаков, начиная с (k+1)-го.
Следствие. Ближайшим целым числа x,
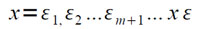
является число
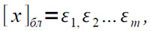
где εi троичные цифры.
Свойство 2. Для представления чисел в данной троичной системе не требуется специального знакового разряда — знак числа определяется знаком старшей значащей троичной цифры.
Эти свойства троичной системы могут эффективно использоваться не только при построении вычислительной машины, но и при программировании. Так, при реализации режима плавающей запятой с помощью подпрограмм во многих случаях либо совсем не приходится заботиться о достижении наилучшей точности — она получается автоматически, либо решение этой задачи значительно упрощается по сравнению с решением ее на машине, использующей двоичную систему счисления. Это связано с тем, что при сдвиге числа вправо (например, при выравнивании порядков в операции сложения с плавающей запятой) наилучшее округление получается без каких-либо дополнительных действий (на основании свойства 1). Симметричное расположение интервала ошибок округления относительно нуля приводит и к тому, что разные ошибки (например, ошибки в представлении констант) часто компенсируют друг друга. Все это приводит к тому, что на машине «Сетунь» можно построить подпрограммы для выполнения действий с плавающей запятой и вычисления элементарных функций с полной вычислительной погрешностью, не превосходящей двух единиц младшего разряда мантиссы [7].
Простой способ выделения ближайшей целой части числа на основании следствия свойства 1) позволяет заметно упростить алгоритмы вычисления экспотенциальной и тригонометрических функций [7].
В силу свойства 2 любая часть числа, содержащаяся в его последовательных разрядах, имеет свой знак, может быть, отличный от знака самого числа. Поэтому каждое число можно рассматривать как последовательность нескольких чисел меньшей разрядности, над которыми можно производить параллельно некоторые действия, например, складывать или вычитать две такие последовательности.
Так, в программе перевода чисел из троичной системы в десятичную при переходе от записи числа вида X·3p к записи вида Y·3q промежуточные значения троичного и десятичного порядков записываются в одной ячейке и изменяются одновременно.
Свойство 2, вообще, сильно упрощает действия с относительными числами. В частности, содержимое любого регистра (например, индекс-регистра) совершенно автоматически рассматривается как относительное число, что удобно само по себе и содержит дополнительные возможности при программировании. По той же причине операции сдвига и нормализации при всей простоте их реализации в машине является весьма универсальными и сильно упрощают программирование действия с масштабами и с плавающей запятой [7]. Так, нормализация величины x=X·3p может быть выполнена при ее пересылке на другое место (например, на место величины y=Y·3q ) без увеличения числа команд:
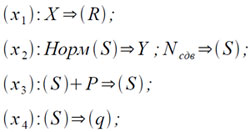
Использование в машине троичной системы счисления заметно сказалось и на ее системе команд. Помимо учета особенностей представления чисел здесь обыгрывается также ряд троичных ситуаций (например, наличие трех видов условных переходов или модификации команд в двух направлениях). Особенности программирования, связанные с системой команд, рассматриваются в следующем пункте.
3. Для выделения какой-либо части числа в системе команд имеется специальная операция поразрядного умножения (операция 20). Эта операция по назначению совпадает с операцией поразрядного логического умножения в машинах, использующих двоичную систему счисления, но значительно богаче последней по возможности. Так, с помощью этой операции можно не только извлечь любую часть слова, подобрав в качестве второго операнда константу с единицами в тех разрядах, которые соответствуют извлекаемым разрядам заданного слова, но можно извлечь эту часть и с противоположным знаком, заменив в константе «извлечения» все единицы на «минус единицы».
(1). Таким образом эта операция может использоваться и для изменения знака у всего числа. Более того, подобрав соответствующую константу можно извлечь часть слова со своим знаком, а часть с противоположным. Это эффективно используется, например, при реализации операции деления [7]. С помощью этой операции легко получить значение функции:
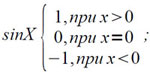
поразрядным умножением нормализованной мантиссы числа на число 1. Модуль числа X может быть получен с помощью соотношения:
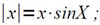
Эти приемы в значительной степени компенсируют отсутствие в системе команд машины «Сетунь» каких-либо операций над знаками чисел.
Для разветвления вычислительного процесса в системе команд машины имеется три вида команд условного перехода, выполняемых по-разному в зависимости от значения признака ω. Этот признак может принимать одно из трех значений 0, 1 и -1, которое вырабатывается как значение функции sign от результата каждой команды (при выполнении некоторых команд сохраняется предыдущее значение признака ω). Для каждого на этих значений имеется свой вид команд условного перехода, которые только при этом значении ω) передают управление по адресу, указанному в команде (в остальных двух случаях управление переходит следующей по порядку команде). Это позволяет во многих случаях использовать для разветвления вычислительного процесса «естественное» значение ω получаемое при вычислении значений основных переменных не прибегая к дополнительным командам для получения нужного значения ω «искусственным» путем. Для этого достаточно бывает выбрать нужный вид команды условного перехода.
Весьма удобными эти команды условного перехода бывают при выборе одного из трех путей в зависимости от того, меньше ли нуля, равно ли нулю или больше нуля какое-либо значение. В этом случае сначала выписываются команды, получающие требуемое значение, за которыми должны следовать подряд две команды условного перехода (при выполнении этих команд сохраняется предыдущее значение ω), например:
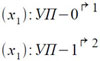
(Здесь в случае нулевого значения осуществляется переход по стрелке ↱1 , в случаe положительного значения — по стрелке ↱2 , а в случае отрицательного значения — к команде x3).
Большую роль при выборе алгоритмов вычисления тех или иных функций играет наличие в системе команд машины «Сетунь» команды умножения вида:
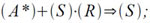
с помощью которой эффективно вычисляются полиномы по схеме Горнера, а именно: каждое выполнение такой команды реализует один шаг схемы Горнера, если в ячейке А* находится очередной коэффициент полинома, в регистре R помечен его аргумент, а в регистре S хранится результат выполнения каждого шага схемы Горнера. Если к этому добавить, что схема Горнера обеспечивает, как правило, весьма медленное накопление ошибок округления, а также, если учесть, что в наборе операций машины отсутствует операция деления, то все это в большинстве случаев делает использование полиномов наиболее эффективным по сравнению с другими методами вычисления функций.
Как известно, автоматическая модификация команд (наличие индекс-регистра) удобна при программировании. С помощью такой модификации очень просто реализуются различные циклы. Например, вычисление значения полинома n-ой степени:
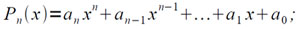
по схеме Горнера в режиме фиксированной запятой описывается с помощью следующей программы:
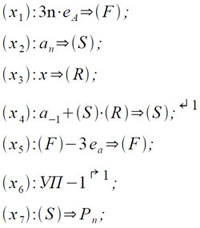
Здесь предполагается, что коэффициенты ai расположены, начиная с a0 в последовательных длинных ячейках памяти; eA обозначает единицу адресной части команды (3eA — разность между адресами двух последовательных длинных ячеек); a-1 — обозначает величину, расположенную в памяти «на расстоянии» (F) от величины a-1 (хранящейся в ячейке, предшествующей ячейке для a0), т.е. при выполнении команды (x4) используется автоматическая модификация ее адресной части.
Примечание. Несмотря на компактность программы вычисления значения полинома с помощью цикла он практически не используется при вычислении значений элементарных функций, так как там степень используемых полиномов обычно не выше 5÷8. Тогда простое перечисление команд вида (3.1) дает не менее компактную (с учетом требуемых констант), но значительно более быстродействующую программу, особенно, если аргумент полинома предварительно вычисляется (получается в регистре S). В последнем случае пересылка аргумента полинома из регистра S в регистр R совмещается с операцией умножения (операция 40) и тогда начало указанной программы будет выглядеть следующим образом: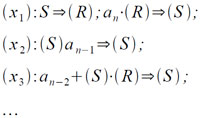
Эффективно используется индекс-регистр и при обращении к подпрограммам или при реализации режима интерпретации для настройки определенных команд по параметрам, задаваемым при обращении. Это достаточно полно проиллюстрировано в статье [1] при описании ИП-2.
Однако наиболее интересна имеющаяся в машине «Сетунь» возможность модификации команд в двух направлениях (содержимое индекс-регистра может как добавляться к адресной части команды, так и вычитаться из нее), значительно повышающая эффективность использования индекс-регистра. Наряду с тем, что в индекс-регистре может находиться как положительное, так и отрицательное значение, это дает возможность использовать для модификации команд значения с тем знаком, с которым его необходимо или удобнее получать в той или иной части программы (например, с точки зрения экономии констант). В ряде случаев одновременное использование модификации команд в разных направлениях (по одному и тому же содержимому индекс-регистра) позволяет создать весьма компактные алгоритмы за счет применения весьма своеобразных приемов. Например, для вычисления каждой из функций:
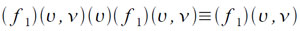
можно воспользоваться одной и той же частью программы, если в командах использующих одну из величин υ и ν записать πF = 1 в командах, использующих другую из этих величин, записать πF = ͞1 и посылать в регистр F нуль или разности между адресами величин υ и ν в зависимости от того, какую из этих двух функций нужно вычислить. Именно такой прием используется в подпрограмме сложения чисел с плавающей запятой [7]. Другой пример своеобразного использования индекс-регистра будет приведен в пункте 4 при рассмотрении алгоритма перевода чисел из троичной системе счисления в десятичную.
Следует особо рассмотреть способы формирования обратной связи при обращении к под-программам. Для этой цели в машине имеются два вида команд:
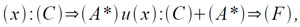
вслед за которыми обычно следуют команды безусловного перехода к подпрограммам. Команда первого вида позволяет зафиксировать место обращения к подпрограмме в некоторой ячейке памяти, команда же второго вида позволяет по существу получить в индекс-регистре при обращении к подпрограмме адрес возврата в основную программу. В первом случае выход из подпрограммы осуществляется двумя командам:
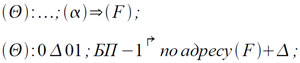
где α — адрес ячейки, в которой зафиксирован адрес x места обращения, а Δ — стандартная поправка к адресу x, являющаяся пo-существу относительным адресом возврата в основную программу (привязанным к месту обращения). Во втором случае для выхода из подпрограммы отводится рабочая ячейка θ и в начале подпрограммы выполняется команда вида:
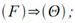
Здесь следует заметить, что в машине «Сетунь» операции безусловного перехода специально был присвоен номер 00, а при записи из регистра F в младших разрядах ячейки памяти формируются нули, так что для выхода из подпрограммы в последнем случае достаточно выполнить (θ) в качестве команды. Хотя эти два варианта почти равноценны, все же в разных ситуациях правильный выбор одного из этих вариантов может привести к некоторой экономии в использовании оперативной памяти, что при ее малой емкости может сыграть решающую роль при реализации тех или иных замыслов. Это имело место, например, при разработке интерпретирующих программ (см.[1], а также пункт 7). Различие между этими способами состоит в том, что при первом способе сохраняется информация в индекс-регистре при входе в подпрограмму, а при втором — при выходе из нее. Кроме того, при первом способе всегда требуется одна рабочая ячейка α, при втором же способе требуется константа, используемая для формирования адреса возврата, зато ячейка θ может использоваться в качестве рабочей вне подпрограммы. Поэтому вопрос о выборе способа обращения может разрешить такой незначительный факт, как наличие рабочей ячейки, свободной на время выполнения подпрограммы, или заранее запасенной константы для формирования адреса возврата.
Второй способ обращения допускает и более простую организацию выхода из подпрограммы, если при ее выполнении не используется индекс-регистр. В этом случае не следует запоминать в начале подпрограммы содержимое индекс-регистра, нужно лишь после выполнения подпрограммы выполнить команду:
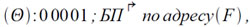
являющейся одновременно и весьма употребительной константой.
На машине «Сетунь» часто приходится использовать пятиразрядные (адресные) константы для изменения содержимого индекс-регистра или в операциях сдвига. В качестве такой константы можно брать любое короткое слово, адресная часть которого имеет требуемый вид, так как младшие разряды не имеют значения при выполнении таких операций. Поэтому адресные константы во многих случаях можно «организовать» за счет соответствующего распределения памяти — достаточно, чтобы к ячейке с адресом, равным требующейся адресной константе, было обращение в какой-либо команде. Тогда такую команду можно использовать и в качестве адресной константы. Обратим внимание еще на несколько неприятную особенность программирования на машине «Сетунь», связанную с тем, что адреса двух последовательных коротких ячеек отличаются на eA если они образуют одну длинную ячейку, и на 2eA – в противном случае. Это несколько усложняет процесс переадресации коротких ячеек. Однако, необходимость в этом возникает сравнительно редко. К тому же в ряде случаев переадресацию коротких ячеек можно заменить переадресацией длинных ячеек (на 3eA), если соответствующие короткие слова располагать либо только в первых, либо только во вторых коротких ячейках, соответствующих последовательным длинным ячейкам. В тех же случаях, когда этим воспользоваться нельзя (например, в интерпретирующих программах [1]), соответствующую переадресацию можно производить согласно следующему соотношению:
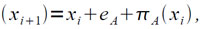
где xi и xi+1 — адреса двух последовательных коротких ячеек, πA(xi) — значение младшего разряда адреса xi. Это реализуется следующими командами:
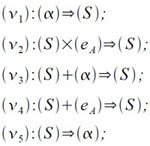
Здесь в ячейке α хранится значение очередного адреса xi.
4. Заслуживает специального рассмотрения алгоритмы перевода чисел из десятичной системы счисления в сокращенную троичную вручную, т.е. средствами десятичной арифметики, и из троичной системы в десятичную с помощью машины, т.е. средствами троичной арифметики.
Особенности алгоритмов перевода первого типа достаточно проиллюстрировать для случая, когда переводимое число x удовлетворяет неравенству:
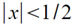
(4.1)
Ясно, что в троичной системе такое число с заданной степенью точности будет иметь вид:
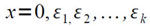
т.е., где εi — троичные цифры, которые необходимо определить. В силу следствия свойства 1 цифра εi обозначает ближайшую целую часть числа 3x, т.е.
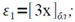
Если положить x1=3x-[3x]бл, мы получим новое число, удовлетворяющее условию (4.1). Отсюда, положив х=x0, можно выписать следующие рекуррентные соотношения для получения троичных цифр εi:
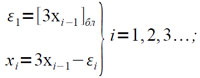
(4.2)
Рассмотрим теперь перевод числа x в десятичную систему с помощью машины. Пусть сначала
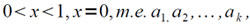
(4.3)
где ai — десятичные цифры, которые нужно определять. Очевидно, что десятичные цифры ai определяются из следующих рекуррентных соотношений:
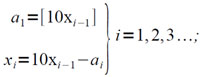
(4.4)
где x0=x. Однако для машины «Сетунь» удобно этот процесс выразить через операции выделения ближайшей целой части и соответствующей ей дробной части:
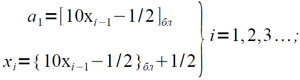
(4.5)
где {υ}бл= υ – [υ]бл. Делая обозначение:
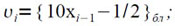
получаем
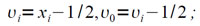
Отсюда
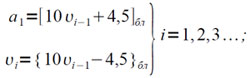
(4.6)
В машине эти формулы могут быть реализованы с некоторыми масштабными множителями. Так как для представления значения любой цифры ai в общем случае потребуется три троичных разряда, то нужно условно перенести запятую в машине на один разряд вправо, т.е. получать значения цифр, уменьшенными в три раза:
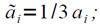
Будем обозначать:
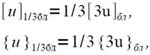
причем операции выделения [υ]1/3бл и {υ}1/3бл реализуются на машине «Сетунь» не сложнее, чем операции выделения [υ]бл и {υ}бл. Тогда соотношения (4.6) можно переписать в виде:
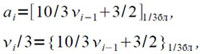
Обозначая ṽi =9vi, Получим:
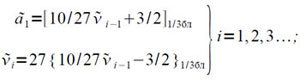
(4.7)
Эти соотношения реализуются на машине весьма простой программой, особенно, если их переписать еще в виде:
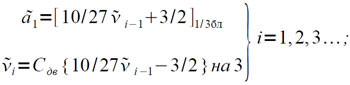
(4.8)
Заметим, что значение выражения
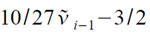
получается в регистре S с помощью одной команды вида:
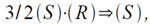
если (S) = ṽi-1, а (R) = 10/27
В случае, когда x является произвольным числом, представленным с плавающей запятой (или с плавающими масштабами) в виде:
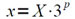
(4.9)
то его необходимо сначала представить в виде
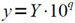
(4.10)
после чего перевод |Y| в десятичную систему совпадает с выше описанным процессом. Что касается величины q, то при сравнительно небольших по модулю значениях она может использоваться, например, как указатель позиции, после которой нужно поставить десятичную запятую (точку) в полученной последовательности десятичных цифр изображения Y. В этом случае не требуется какого-либо ее перевода в десятичную систему счисления. В общем случае величину q, может оказаться необходимым перевести в десятичную систему счисления в качестве десятичного порядка числа x, однако этот процесс можно свести, например, к последовательному вычитанию из q по 10 единиц и подсчету числа десятков, так как в худшем случае q будет представляться двузначным десятичным целым числом.
Процесс перехода от записи вида (4.9) к записи вида (4.10) называется десятичной нормализацией числа x. При реализации его на машине удобно сначала получить z=1/2•x в виде:
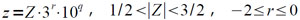
(4.11)
так как при этом удобно использовать операцию нормализации. После этого достаточно положить Y = 2/3Z•3r, чтобы перейти к записи (4.10), причем можно показать, что здесь:
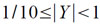
Однако, удобнее получать Ỹ = 3Y = 2Z•3r так как множитель 3 легко учитывается при переводе |Y| в десятичную систему. Процесс перехода от записи вида:
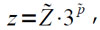
Где Z̃ = норм(1/2 X), P̃ = p+N, N — число сдвигов при нормализации 1/2 X, к записи вида (4.11) производится следующим образом. Сначала проводится серия преобразований по формулам:
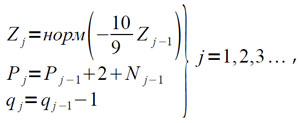
(4.12)
где Nj-1 — число сдвигов при нормализации 10/9 Zj-1, Z0 = Z̃, P0 = P̃, q0 = 0 до тех пор, пока впервые не выполнится условие Pj ˃0 при некотором j = j0. Затем проводится серия преобразований по формулам:
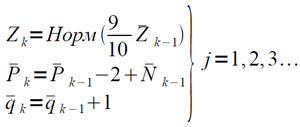
(4.13)
где N̅k−1 — число сдвигов при нормализации 9/10 Z̅k-1, Z̅0 = Zj0, P̅0 = Pj0, q̅0 = qj0 до тех пор, пока впервые не выполнится условие P̅k ≤ 0 при некотором k = k0.
Очевидно, что -2 ≤ Pk0 ≤ 0.
Следовательно, мы придем к записи вида (4.11), причем:
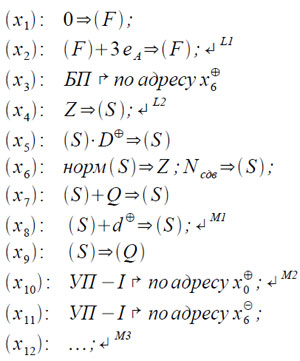
Процесс построения записи (4.11) реализуется на машине весьма компактной программой с использованием модификации команд по (F) в обоих направлениях. Эта программа имеет следующий вид:
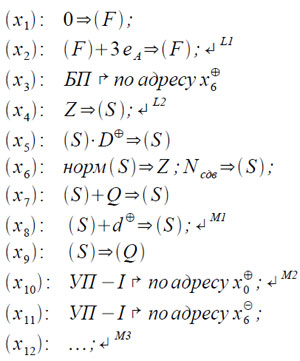
Здесь команда (x3), (x5), (x8) и (x10) перед выполнением модифицируются добавлением (F), т.е. они имеет ,команда же (x11) перед выполнением модифицируется вычитанием (F), т.е. она имеет πF = ͞1 . Величина Z последовательно обозначает текущие значения величин Zj и Zk (первоначально Z =Z̃). Величина Q является длинным словом, составленным из пары значений р и q (в первой половине — р, а во второй — q), причем p последовательно обозначает текущие значения величин pj и p̅k, а q — текущие значения величин qj и q̅k. Для упрощения программам была исключена возможность получения Q=0 за счет уменьшения p на 1/3 eA (величина р — целая и представляется в машине кратной eA). Величины D и d — фиктивные. В памяти машины расположены константы 10/9 и 9/10 на расстоянии 3eA и 6eA от величины D и константы d1 и d2= -d1 на расстоянии ЗeA и 6eA от величины d, где d1 является длинным словом, в первой половине которого записано 2eA, а во второй половине — «минус единица» для изменения q (-eq). Переход по адресу x6 в команде (x3) никогда не выполняется, так как эта команда будет выполняться при (F) ≠ 0 и первый раз при (F)=3eA она передаст управление по адресу x8 (по стрелке ↱M1). В связи с этим к моменту выполнения данной программы в региcтре S должно быть получено длинное слово S1 + S2•3-7, причем
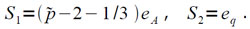
Тогда после первого же выполнения команд (x8) и (x9) величине q будет присвоено первоначальное значение:
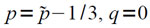
Особенностью этой программы является наличие в ее конце двух команд условных переходов, модифицируемых по (F) в разных направлениях. Пока выполняется серия преобразования по формулам (4.12), команда (x10) будет пропускать управление следующей команде, а команда (x11) в силу Q≠0 будет передавать управление по адресу x4 (по стрелке ↱L2) при (F) = 3eA. При первом же выполнении условия р > 0 команда (x10) передаст управление по адресу x2 (по стрелке ↱L1), в результате чего осуществится переход к серии преобразований по формулам (4.13) из-за того, что будет положено (F) = 6eA. При этом команда (x3) передаст управление уже по адресу x10 (сохранив ω=1), а команды (x10) и (x11) поменяются своими ролями. Как только теперь выполнится условие p≤0, управление придет к команде (x11), которая передаст управление по адресу x2 и тем самым прекратит вторую серию преобразований. При (F) = 9eA произойдет выход из данной программы по команде (x3), которая передаст управление по адресу x12.
Алгоритмы переводов из троичной системы счисления в десятичную вручную и из десятичной системы в троичную с помощью машины здесь никаких особенностей не имеют и сводятся к вычислению значений соответствующих полиномов.
5. Имеющаяся в машине «Сетунь» оперативная память емкостью в 162 коротких слова позволяет решать без использования магнитного барабана лишь самые простейшие задачи. Именно на таких задачах и реализуется средняя оперативная скорость в 4800 операций в секунду. Основным же видом памяти в машине «Сетунь» является магнитный барабан емкостью в 1944 коротких слова (36 зон по 54 коротких слова), который реализован в качестве внешнего запоминающего устройства. Частые обращения к барабану могут значительно снизить быстродействие машины, так как каждое обращение к нему занимает в среднем 7500 мксек, что, примерно, эквивалентно времени выполнения 35 команд с использованием только оперативной памяти. Однако, обмен информацией между оперативной памятью и магнитным барабаном производится по зонам (по 54 коротких слова), поэтому во многих случаях при программировании можно так организовать счет и так разместить информацию, в памяти машины, чтобы между обращениями к барабану производился значительный объем вычислений (переработки информации). За счет этого можно добиться сравнительно небольшого снижения быстродействия при использовании магнитного барабана.
Для иллюстрации такого использования магнитного барабана рассмотрим класс задач, при решении которых требуется хранить в памяти сравнительно небольшое число переменных, хотя получение искомых результатов может быть связано с весьма сложными вычислениями. В этом случае целесообразно все эти переменные, а может быть и исходные данные, постоянно хранить в оперативной памяти (лишь бы они занимали не более двух зон). Вся же программа вычислений может храниться на магнитном барабане, в оперативной памяти для нее достаточно отвести одну зону, в которую будут поочередно вызываться части программы, подлежащие выполнению. Тогда перед вызовом в оперативную память каждой новой зоны программы будет как бы производиться задержка в ее выполнении, примерно, на 35 тактов, для выполнения же вызванной зоны при отсутствии в ней циклов потребуется до 54 тактов работы машины. Так как при решении таких задач не будет никаких других обращений к барабану, то указанное использование барабана снижает быстродействие машины, примерно, 1,5÷2 раза, при наличии же в зонах программы циклов снижение быстродействия машины может быть еще меньше, а в ряде случаев оно может практически отсутствовать, если такие циклы будут встречаться часто или будут выполняться при большом числе повторений (при этом барабан используется существенно для хранения программы). Такая ситуация встречается, например, при вычислении интегралов (особенно многократных).
При реализации на машине такой схемы использования барабана каждая зона программы после выполнения должна будет сама вызывать следующую часть программы, причем в ту же самую зону оперативной памяти. Для этого достаточно выполнить всего лишь одну команду:
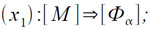
(5.1)
где М – зона магнитного барабана содержащая очередную зону программы, а Фα – зона оперативной памяти, отведенная для выполнения программы. Тогда после выполнения команды (x1) должна будет выполняться команда (x2), однако эта команда будет уже принадлежать другой зоне программы, которую по команде (x1) вызвала «на себя» только что выполнившаяся зона программы. Поэтому выполнение команды (x1) равносильно безусловному переходу по адресу x2 в зону программы M. Этот прием широко используется при программировании на машине «Сетунь».
Если в какой-либо зоне программы имеются переменные команды, то, естественно, состояние этой зоны после ее выполнения необходимо запоминать на магнитном барабане, если при ее выполнении были изменены эти переменные команды. Для этого в такой зоне перед командой вызова следующей зоны должна выполняться команда:
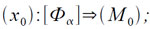
(5.2)
где М0 — зона магнитного барабана, отведенного для данной зоны программы. Очевидно, что такая же ситуация возникает в том случае, когда внутри какой-либо зоны программы имеются рабочие ячейки для хранения промежуточных результатов.
Во многих случаях удобно команду вида (5.1), а в случае необходимости и расположенную перед ней команду вида (5.2), помещать в самом начале зоны программы и передавать туда управления по окончании выполнения данной зоны. Тогда каждая зона программы будет начинать выполняться с одного и того же места. Рассмотренный прием позволяет реализовать любое разветвление вычислительного процесса, однако ниже будет рассмотрен более общий прием, удобный для программ со сложной структурой.
Другой класс задач, эффективно решаемых на машине «Сетунь» составляют задачи последовательной обработки данных измерений или другого потока информации по сравнительно несложным формулам. Программу решения такой задачи часто можно полностью разместить в оперативной памяти, оставляя одну из ее зон для обрабатываемых данных (в крайнем случае, возможна редкая смена зон программы в оперативной памяти). Обращение к барабану при решении такой задачи производится в основной лишь для вызова в оперативную память очередной группы (зоны) данных (для их обработки) и для записи полученных промежуточных результатов (обработанных данных) обратно на барабан. Ясно, что такое использование барабана не может сколько-нибудь заметно снизить быстродействие машины, так как преобразование каждого короткого или длинного слова требует даже в простейших случаях выполнения нескольких команд, а каждый обмен информацией с барабаном связан с преобразованием 54-х или 27-ми таких слов. Аналогичная ситуация может возникнуть и при решении более сложных задач на отдельных этапах вычислительного процесса. В этих случаях также целесообразно для уменьшения общего времени счета задачи воспользоваться описанной схемой.
В более общем случае память машины можно использовать следующим образом. Программу и всю информацию, необходимую для ее выполнения, кроме некоторых наиболее употребительных величин и констант, будем размещать на магнитном барабане. Одну из зон оперативной памяти, например, Ф1, отведем для выполнения очередной зоны программы, вызываемой с магнитного барабана, так же, как это было описано выше для первого класса задач. Другую зону оперативной памяти, например, Ф0, будем использовать в качестве места, на которое будет вызываться с магнитного барабана информация, требующаяся при выполнении программы (так же, как и при решении задач второго из описанных классов). Естественно, что программа при этом должна обеспечить как своевременную смену в оперативной памяти зон программы, так и вызов с барабана и запись на него информации, преобразуемой по ходу выполнения программы. При этом обращения к барабану могут производиться весьма часто. Однако число таких обращений можно заметно уменьшить, если в третьей зоне оперативной памяти (в зоне Ф-1) разместить наиболее употребительные константы, а также такие переменные, которые наиболее часто изменяются или используются в процессе вычислений. Кроме того, целесообразно в зону Ф0 вызывать для выполнения наиболее употребительные подпрограммы (например, подпрограммы вычисления элементарных функций).
При реализации этой схемы использования машины возникает еще вопрос о способах обращения к подпрограммам и вопрос о способах разветвления вычислительного процесса в самых общих случаях. Однако способы обращения к подпрограммам достаточно полно описаны в литературе [3, 5, 6], особенности же организации обратной связи на машине «Сетунь» были уже рассмотрены в пункте 3. На втором вопросе следует несколько остановиться. Он полностью сводится к вопросу о реализации безусловных переходов от одной зоны программы к другой. Хотя указанные при рассмотрении первого класса задач способы реализации безусловных переходов позволяют запрограммировать решение любой задачи, для которой емкость памяти машины будет достаточной, все же следует указать другой, вполне универсальный и в ряде случаев более удобный способ. Для этой цели в зоне Ф-1 нужно поместить небольшую подпрограмму, реализующую этот безусловный переход. Если обращение к этой подпрограмме производить следующим образом:
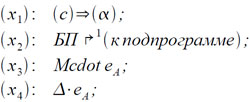
где α обозначает рабочую ячейку, М — номер зоны программы на магнитном барабане, а Δ — номер строки в этой зоне, куда нужно передать управление, то указанная подпрограмма будет иметь вид:
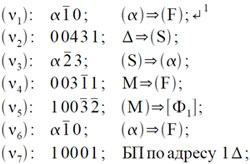
В некоторых случаях можно сократить время обращения к барабану за счет «оптимального» размещения информации на барабане и тщательного подбора моментов обращения к нему. Это связано с тем обстоятельством, что барабан разбит на 4 сектора относительно своей окружности так, что каждому сектору принадлежат 9 зон. Время обращения к барабану складывается из времени ожидания нужной зоны (нужного сектора) и времени непосредственной передачи информации. Так как барабан делает полный оборот за 10000 мксек, то время ожидания колеблется от 0 до 10000 мксек, а время непосредственной передачи информации всегда равно 2500 мксек. Таким образом, время обращения зависит как от номера зоны, к которой производится обращение, так и от момента обращения, поэтому при программировании можно попытаться свести к минимуму суммарное время ожидания при всех обращениях к барабану. В частности, если при обращении к некоторой зоне барабана нам будет известно, что 27 в этот момент потребуется 5000 мксек на ее ожидание, то можно отложить обращение к этой зоне и выполнить за счет времени ожидания некоторые действия (требующие для выполнения не более 5000 мксек), а затем уже произвести обращение к этой зоне. В результате этого мы указанные действия выполним без дополнительных затрат времени или, что то же самое, существенно уменьшим время ожидания при обращении к этой зоне. Распределения зон по секторам указано в следующей таблице:
|
Сектор |
Номера зон |
|
I |
1 ͞4÷ 14 |
|
II |
2 ͞4 ÷ 24 |
|
III |
3 ͞4 ÷34 |
|
IV |
4 ͞4 ÷14 |
В процессе вращения барабана сектора проходят под считывающими (записывающими) магнитными головками в следующем порядке: I, II, III, IV, I и т.д.
Отсюда следует, что при обращении, например, к сектору IV сразу же после обращения к сектору I время ожидания будет равно 5000 мксек, после обращения к сектору II — 2500 мксек, а после обращения к тому же сектору IV — 7500 мксек. Однако, нужно иметь в виду, что при обращении к предыдущему (по порядку прохождения под магнитными головками) сектору время ожидания будет равно не нулю, а 10000 мксек, например, при обращении к сектору I после обращения к сектору IV или к сектору III после обращения к сектору II.
6. Наличие в машине алфавитно-цифровых устройств ввода и вывода позволяет задавать машине информацию, а также получать результаты в любой желаемой для заказчика форме. В частности, на машине можно получать таблицы, удовлетворяющие всем требованиям, предъявляемым при типографском издании: таблицы могут быть разбиты на страницы, на каждой странице может быть любое число столбцов результатов, которое может быть размещено на стандартном листе бумаги, результаты могут выдаваться с любым числом знаков, соответствующим точности вычислений, и выдаваться в любой привычной для человека форме, наконец, каждая страница может быть снабжена соответствующим заголовком. И дело здесь не только в том, что машина может печатать буквы и некоторые знаки, а еще и в том, что на машине «Сетунь» отказались от принципа выдачи чисел с заранее закрепленным форматом (от принципа, принятого на большинстве существующих в настоящее время в Советском союзе машин). Выдача каждого символа на машине «Сетунь» должна программироваться, при этом может (и должно) программироваться оставление нужного числа пробелов между числами и другими группами символов (например, словами), а также переход к печати новой строки или оставление чистыми некоторых строк. Одна из систем подпрограмм (процедур) ввода и вывода, обеспечивающая реализацию этих возможностей, описана в статье [8].
С помощью таких печатающих устройств можно выводить результаты в виде графиков, если рассматривать номер строки в качестве абсциссы, а номер позиции в строке в качестве ординаты координатной системы и печатать в определенной позиции (зависящей от значения выдаваемой на график функции) каждой строки какой-либо знак, например, точку. Однако, хотя это и может сэкономить ручной труд, является все же недостаточно эффективным использованием машины. Более эффективно использование таких печатающих устройств для построения карты уровней (рельефа) значений некоторой функции от двух переменных. В этом случае каждая позиция каждой строки может рассматриваться как узел некоторой сетки значений этой функции (значением двух переменных поставлены в соответствии номера позиции и строки). Диапазон изменения значений функции разбивается на ряд отрезков (уровней), каждому из которых ставится в соответствии некоторый символ (цифра, буква и т.п.). В каждой позиции карты печатается символ, соответствующий отрезку, к которому принадлежит значение функции в данном узле. Наличие в машине возможности печатать каждый символ, как черным, так и красным цветом позволяет фиксировать значение уровня с точностью почти до одного процента. Например, удобно интервал значений разбивать на 81 уровень, 40 из которых обозначать черными символами, 40 других — красными и один (обычно, средний) — пробелом. Следует заметить, что если получаемая при этом точность и форма вывода устраивает заказчика, то такой способ вывода результатов может сильно уменьшить время вывода, так как вместо каждого значения выдается на печать всего лишь один символ. Использование данного способа в конкретной задаче описано в статье [9].
Алфавитно-цифровые устройства ввода и вывода широко используются при автоматическом программировании. Они позволяют выработать язык программирования (автокод), удобный для человека и близкий к обычным математическим обозначениям, причем программы, записанные на этом языке, могут непосредственно вводиться в машину, а затем переводится на язык машины с помощью специальных программ (автопереводчиков, трансляторов и т.п.). Кроме того, эти устройства облегчают использование машины, например, для аналитических выкладок.
При обработке символов часто приходится выбирать один из путей переработки информации в соответствии с исследуемым символом. Так как каждый символ кодируется в машине некоторым целым числом (положительным, отрицательным или равным нулю), то целесообразно для разветвления процесса переработки иметь таблицу безусловных переходов, такую, чтобы для любого i, кодирующего некоторый символ, в i-ой строке этой таблицы был размещен безусловный переход, соответствующий этому символу. Такую таблицу переходов обычно называют переключателем. Тогда требуемое разветвление процесса переработки информации реализуется с помощью следующих команд:
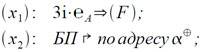
где a — адрес нулевой (при i=0) строки переключателя. При этом предполагается, что переключатель образуют либо только первые, либо только вторые короткие слова каждой длинной ячейки и величина 3i•eA уже получена в какой-либо ячейке памяти. Аналогичным образом реализуется набор информации в зависимости от исследуемого символа. Например, если информация, соответствующая каждому символу, задается одним длинным словом, то все эти слова можно расположить в последовательных ячейках в виде таблицы, связанной с исследуемыми символами так же, как и переключатель. Тогда выбор требуемого слова реализуется с помощью команд:
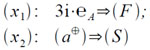
Обратная задача — выбор группы символов по некоторому целому числу К. — решается так же, если эта группа символов размещается в одной длинной (или короткой) ячейке. Это используется, например, при составлении карты уровней. Указанные приемы программирования подробно описаны в литературе [5].
7. Система математического обслуживания, разработанная для машины «Сетунь», учитывает основные особенности этой машины. Так здесь оказалось целесообразным использование несложных интерпретирующих программ. Позволяя значительно улучшить аппарат программирования, они сравнительно несильно снижают производительность машины в связи с тем, что значительная часть интерпретации производится за счет времени ожидания нужной зоны магнитного барабана (а к барабану производятся только самые необходимые обращения). Например, использование интерпретирующей системы с ИП-2 [1] снижает производительность машины не более, чем в 3-3,5 раза.
Для обслуживания основных классов вычислительных задач разработаны четыре варианта интерпретирующих систем. Система с ИП-2 предназначена для ведения вычислений с плавающей запятой или с плавающими масштабами [4], примерно, с восемью верными десятичными знаками. Система с ИП-3 предназначена для ведения вычислений с плавающей запятой, примерно, с шестью верными десятичными знаками, но с более компактным, чем в ИП-2, представлением чисел. Обе эти системы обслуживают весьма близкие классы задач. Вторая система не производительнее первой и обеспечивает вычисления с меньшей точностью, поэтому почти везде, где емкость памяти оказывается достаточной, целесообразно использовать ИП-2. Кроме того, в первой системе можно вести вычисления с плавающими масштабами, что в ряде случаев может позволить добиться высокого быстродействия. Вторая система, кроме случаев, когда при подготовке задачи к решению, ощущается недостаток памяти, удобна также и тогда, когда приходится производить действия не только над числами с плавающей запятой, но и над машинными словами (длинными или короткими) самого различного происхождения, например, над числами с фиксированной запятой или над группами символов. Это связано с тем обстоятельством, что ИП-З, в отличие от ИП-2, рассматривает каждый операнд любой операции как одно машинное слово, при вызове которого в стандартные ячейки не производятся его нормализации (все числа с плавающей запятой в системе ИП-З предполагаются всегда нормализованными). При этом систему с ИП-З, возможно нужно будет пополнить дополнительными подпрограммами, или, вообще, на базе ИП-З можно создать новую систему без подпрограмм, реализующих арифметику о плавающей запятой.
Более удобна ИП-З также и в тех случаях, когда приходится оперировать о векторами (или, вообще, массивами). Действительно, в ИП-2 каждое число занимает две ячейки (длинную и короткую), причем обе эти ячейки должны находиться в одной зоне. Поэтому здесь возникают некоторые трудности в размещении компонент вектора в нескольких зонах. Этот дефект отсутствует в системе с ИП-3, так как в ней каждое число занимает одну длинную ячейку.
Третья система, система с ИП-4, предназначена для действий с комплексными числами [I0]. Хотя в этой системе каждое действие выполняется в среднем раза в два медленнее, чем в предыдущих системах, однако эти действия значительно более содержательные. Поэтому использование этой системы в тех задачах, где приходится вести вычисления в комплексной плоскости, не только может сильно упростить процесс подготовки задачи к решению на машине, но практически и не приводит к снижению производительности машины.
Система с ИП-5 предназначена для решения с повышенной точностью (примерно, с 12-ю верными десятичными знаками) сравнительно несложных задач (например, получение полиномов наилучшего приближения для каких-либо функций). В ней программным путем реализуются действия над числами, каждое из которых представляется двумя длинными машинными словами (одно короткое слово представляет порядок числа, а три других коротких слова — мантиссу). Вычисления в этой системе будут производиться в два-три раза медленнее, чем в системе с ИП-2 (или с ИП-3). Особенностью этих четырех систем является использование в них режиме частичной интерпретации [I], при котором выполняются обычные машинные команды до тех пор, пока не будет произведено обращение к интерпретирующей программе для выполнения тех или иных действий. Это позволяет создать системы с высокой производительностью, но дает весьма ограниченные возможности для создания удобных систем программирования. Весьма удобный аппарат программирования можно создать при реализации режима полной интерпретации, при котором на машине «Сетунь» будет интерпретироваться другая машина с системой команд, удобной для программирования, а программы будут писаться в коде этой новой машины (в псевдокоде). Использование таких систем целесообразно в таких условиях, когда время на подготовку каждой задачи к решению на машине ограничено, а само время счета этой задачи сравнительно невелико.
Однако, одна из разработанных в настоящее время в Вычислительном центре МГУ интерпретирующих программ такого типа — интерпретатор ПОЛИЗ (польской инверсной записи) — обеспечивает сравнительно высокую производительность и в то же время весьма удобна при трансляции для нас с алгоритмических языков (например, с АЛГОЛа-60). На базе этого интерпретатора разработан автокод, позволяющий составлять программу в алфавитно-цифровой виде, а также создается транслятор с языка АЛГОЛ-60 на язык этого интерпретатора.
Наряду с созданием системы автоматического программирования для такой машины должен быть разработан ряд программ для решения типовых задач, максимально использующих возможности машины. В настоящее время разработаны программы для корреляционного и спектрального анализа статистических данных и для решения некоторых задач структурного анализа кристаллов. Ведутся работы по созданию некоторых других программ.
Цитированная литература:
1. Жоголев Е.А. Система команд и интерпретирующая система для машины «Сетунь». I. вычисл.матем. и мат. физики. т.1, No 3, 1961, 499-512.
2. Брусенцов Н.П., Жоголев Е.А., Веригин В.В., Маслов С.П., Тишулина A.М. Малая автоматическая цифровая машина «Сетунь». Вестник Московского Университета, серия математика, механика, No4, 1962.
3. Жоголев Е.А., Росляков Г.С, Трифонов Н.П.,Шура-Бура М.P. Система стандартных подпрограмм. Под ред. М.Р.Шура-Бура. Физматгиз, 1958.
4. Жоголев Е.А. Маштабирование. Энциклопедия современной техники, серия «Автоматизация производства и промышленная электроника», т.2, Москва, 1963.
5. Мак-Кракен Д.Д. Программирование для цифровых вычислительных машин. ИЛ., Москва, I960.
6. Биркган А.Ю. и Воскресенский Г.П. Программирование для цифровой вычислительной машины «Урал2». «Сов.радио», 1962.
7. Жоголев Е.А. Вычисление элементарных функций на машине «Сетунь», В сб. «Вычислительные методы и программирование. Ш». Издво МГУ, 1964.
8. Бондаренко Н.В. Система подпрограмм для ввода и вывода алфавитно-цифровой информации (выйдет в данной серии).
9. Щедрин Б.М. Программа построения карты уровней электронной плотности. Кристаллография, т.8, вып.6, Москва, 1963.
10. Фурман Г.А. Интерпретирующая система для действий с комплексными числами (выйдет в выпуске 2 данной серии).
Серия: Математическое обслуживание машины «Сетунь»
4 ноября 2014
