Как специальные конструкции трансляции могут порождаться универсальными процессами смешанных вычислений

[1]

М. А. Бульонков, А. П. Ершов

Введение

Фундаментальная связь между трансляцией и смешанными вычислениями задается проекциями Футамуры [1]. Пусть mix(P, X, Y) — процессор смешанных вычислений в языке реализации L, запрограммированный в этом же языке (автопроектор), P — программы в L, X — значения некоторых аргументов в P, Y — имена остальных аргументов в P, при этом

mix(p, x, Y) = p_x(Y),

где p_x(Y)— программа в L с аргументами Y, называемая остаточной программой, или проекцией p на x, и удовлетворяющая соотношению

p_x(y) = p(x, y).

Пусть, далее, Λ = (Σ, Π, Δ) — класс входных языков, где ∑ = {σ} — множество семантик, заданных интерпретаторами, запрограммированными в языке реализации L, Π= {π} — множество программ конкретного входного языка σ и Δ = {δ} — множество данных конкретной входной программы π.

Пусть, наконец, стоит задача: найти общий метод (транслятор трансляторов) cocom(Σ, Π, Δ), позволяющий для любого языка σ построить транслятор comp(Π, Δ), который для любой программы π строит ее объектный код ob(Δ) в некотором объектном подмножестве языка реализации.

Тогда, как известно:

ob(Δ) = mix(σ, π, Δ) = σπ(Δ),	(F1)
comp(π, Δ) = mix(mix, σ, (π, Δ)) = mixσ(π, Δ),	(F2)
cocom(Σ, Π, Δ) = mix(mix, mix, (Σ, Π, Δ)) = mixmix(Σ, Π, Δ),	(F3)

или в словесной формулировке:

объектный код — это проекция интерпретатора на входную программу;
транслятор — это проекция смешанного вычислителя (автопроектора) на интерпретатор;
транслятор трансляторов — это проекция смешанного вычислителя на самого себя.

Найденные в разное время Ё. Футамурой[2], А. П. Ершовым [3] и В. Ф. Турчиным[3] [4] эти соотношения стали общеизвестными после обсуждения их на Рабочей конференции ИФИП и были изложены А. П. Ершовым в [5]. Хотя проблема систематического получения трансляторов из формального описания языков имеет обширную литературу, а термин «компилятор компиляторов» [6] восходит еще к началу 60-х годов, понятие смешанных вычислений дало новый толчок этой важной задаче системного программирования.

Привлекательность проекций Футамуры в их фундаментальности, однородности, автоматичности как в получении транслятора, так и в обосновании его правильности.

В то же время буквальное применение жестких схем смешанных вычислений к интерпретаторам не дает ничего интересного, поскольку из-за избыточных задержек остаточные программы почти не отличаются от исходных. Смешанные вычисления не снимают проблемы систематического построения трансляторов, но подсказывают новые пути к ее решению и в особенности обоснованию.

Впервые получение трансляционной семантики из интерпретационной методом смешанных вычислений на модельном примере демонстрировалось в [5]. Проекция F3 при этом не использовалась; ее эквивалент, упоминавшийся под названием «генерирующее расширение», был описан неформально, ad hoc. Кроме того, ряд тонких моментов, связанных с раскрытием процедур и глобализацией имен, вообще не затрагивался.

На основе работы [5] было выполнено более широкое исследование по получению транслятора из операционной семантики языка методом генерирующего расширения. Оно составило содержание аспирантской диссертации [7] и последующей публикации [8]. В качестве языка реализации был взят Венский язык определений (VDL). Процедура генерирующего расширения содержит много априорных ограничений; интерпретатор входного языка требует предварительной разметки исполняемых и задерживаемых действий; в работе отсутствует указание на программную реализацию генерирующего расширения.

Обещающий эксперимент по получению транслятора из интерпретатора с использованием F3 и F2 описан в [9]. Языком реализации является аппликативное подмножество Лиспа, входной язык — простой язык присваиваний, ветвлений и пока-циклов. Проектируемая программа тоже требует детальной предварительной разметки. Существенно, что операционные характеристики транслятора и объектного кода показывают значительное ускорение по сравнению с чистой интерпретацией. Авторы работы отмечают сложность задачи построения F2 и F3 для императивного языка реализации.

В отмеченных работах преобладал интегральный подход, направленный на конструктивное подтверждение самого факта реализации автопроектора и его применения к трансляции. В нашей работе мы пытаемся углубить анализ проблемы.

Мы описываем новую схему автопроектора, реализующего смешанные вычисления на классе программ, в котором область доступной памяти после частичного задания аргументов становится конечно-определенной, а разбиение памяти на доступную и задержанную не меняется в ходе вычислений [10]. В пределах этого класса, который мы будем называть анализаторными программами, удается разрешить принципиальное противоречие между глубиной и конечностью смешанных вычислений, не налагая ограничений, неизбежных в жесткой схеме универсальных или в разных вариантах специализированных смешанных вычислений.

Главной же целью нашего исследования является выяснение того, как при получении транслятора из операционной семантики языка с помощью универсального процесса смешанных вычислений в нем возникают структуры, специфические для техники трансляции.

Поясним эту цель более подробно. Транслятор — это одна из наиболее отработанных компонент программного обеспечения. Ее фундаментализация постоянно сопровождалась накоплением специальных приемов, найденных в разное время и направленных на повышение эффективности трансляции. Никакая универсальная схема построения трансляторов не сможет конкурировать со штучным производством трансляторов, если в ее недрах не будут естественно возникать те структуры, которые характеризуют развитую и эффективную схему трансляции. До сих пор это было и остается ахиллесовой пятой любого транслятора трансляторов.

Поэтому любой конструктор трансляторов имеет право задать энтузиасту смешанных вычислений много вопросов. Перечислим, не претендуя на полноту, наиболее существенные из них. Все эти вопросы относятся к транслятору, полученному с помощью автопроектора.

Откуда в трансляторе берутся фазы (просмотры) и, в частности, разделение на анализ и генерацию?
Является ли однопросмотровая схема трансляции фундаментальной или вторичной?
Если однопросмотровая схема фундаментальна, то откуда берутся специальные приемы, обеспечивающие однопросмотровость (в частности, косвенную адресацию величин и меток)?
Откуда берутся шаблоны объектных команд при генерации?
Откуда берется таблица символов в трансляторе?
Откуда берется стек в трансляторе?
Можно ли с помощью смешанного вычисления получить разумный транслятор из денотационной или трансформационной семантики входного языка?
Откуда транслятор берет свою операциональность: от смешанного вычислителя или интерпретатора? Если от обоих, то в какой степени от каждого?
Можно ли с помощью одного автопроектора получить версии трансляторов для рекурсивного и одноциклового интерпретатора, которые будут давать идентичный объективный код?
Другими словами, что является реальным инвариантом разных способов задания семантики языка, вносимым в функционирование транслятора?

Для того чтобы добиться чистоты, как в постановке, так и в ответе на эти вопросы, мы считаем необходимым придерживаться следующего методологического принципа. Автор семантики входного языка имеет право знать, что он ее пишет для подачи на вход смешанного вычисления. Конструктор транслятора имеет право знать, что он применяет автопроектор для получения транслятора. Однако автор автопроектора не имеет права знать, что такое техника и приемы трансляции. Все специальные приемы, реализуемые в автопроекторе, должны быть внутренне мотивированы сущностью смешанных вычислений.

§ 1. Автопроектор

Охарактеризуем сначала язык реализации (ЯР), для которого и на котором будет записан автопроектор. Язык будет сильно недоопределен, особенно в части данных и набора базисных операций, однако это не помешает нам придать необходимую конкретность и определенность всем узловым моментам изложения.

Программа на языке реализации — это последовательность помеченных команд с выделенной меткой входа. Текстуальный порядок команд не имеет значения, так как каждая команда назначает себе преемника, явно указывая его метку. Каждая команда состоит из двух частей — действия и назначения преемника, которое в стиле Алгола-60 имеет вид на . Таким образом, априорной особенностью языка реализации является наличие переходов по вычисляемым меткам.

Все детали структурирования данных считаются упрятанными в базовые функции выборки, так что будет достаточно сказать, что все обращения к данным происходят по их именам. Всю совокупность имен, упоминаемых в ЯР-программе, будем называть памятью программы.

Смешанные вычисления в языке реализации определяются для класса так называемых анализаторных программ, для которых постулируется следующее:

перед началом вычислений известно разбиение памяти на заданную, доступную и задержанную (недоступную);
заданная память загружается перед началом вычислений и в последующем не меняется;
область доступной памяти во время вычислений не изменяется;
для любой загрузки заданной памяти множество состояний доступной памяти конечно;
любая функция выборки из заданной памяти однозначно определяется состоянием доступной памяти.

Замечание. Реальными ограничениями являются три последних постулата. Третий постулат подчеркивает, что доступная память используется, главным образом, для обработки информации из заданной памяти; влияние задержанных величин на доступную память ограничено. В универсальных схемах смешанных вычислений область доступной памяти обычно сужается (см., например, [11]) по ходу вычислений. Четвертый постулат обычно соблюдается для всевозможных программных процессоров: подача на вход процессора обрабатываемой программы ограничивает область значений величин процессора множествами всевозможных элементов заданной программы, которые, естественно, конечны, равно как и глубина возникающей при обработке рекурсии. Пятый постулат ограничивает влияние задержанных величин на доступность заданной информации.

В работе [10] описан алгоритм смешанных вычислений для анализаторных программ, в основе которого лежит теоретическая конструкция, требующая размножения исходной программы в количестве экземпляров, равном числу состояний доступной памяти. Смысл этого размножения в том, что каждый экземпляр программы выполняется на фиксированном состоянии доступной памяти. Как только выполняется присваивание, преобразующее
i-е состояние памяти в j-е, в качестве преемника берется соответствующая команда из j-й копии программы. После того как над такой сильно раздутой программой выполнятся стандартные редукции, в остаточной программе остаются только действия с участием задержанных величин.

Реальная организация смешанных вычислений анализаторных программ более экономна. Свяжем с программой граф, вершинами которого являются состояния доступной памяти. Если при каком-либо вычислении в программе возможен переход из i-го состояния доступной памяти в j-е, то в графе проводится дуга от i-й вершины к j-й. Тогда множество достижимых состояний доступной памяти при фиксированной загрузке заданной памяти находится как транзитивное замыкание начального состояния доступной памяти. Именно по принципу построения транзитивного замыкания и работает смешанный вычислитель для анализаторных ЯР-программ.

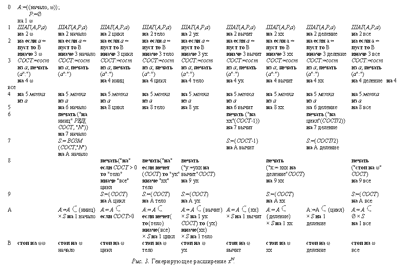
Сделаем необходимые пояснения к ЯР-автопроектору, т. е. к ЯР-программе смешанного вычислителя для языка реализации, показанной на
рис. 1. Будем называть ЯР-программу, поступающую на вход смешанного вычислителя, обрабатываемой программой. Обрабатываемая программа представляется в виде вектора Π, индексируемого метками входной программы. Компонентой вектора программы является команда, помеченная индексирующей меткой и представленная структурой с тремя полями: действием (выполненным командой), источником (если действие является присваиванием) и преемником (именующим выражением, назначающим преемника). Над каждой командой определен синтаксический предикат новсост (новое состояние), отличающий присваивания элементу доступной памяти (т. е. точки изменения состояния доступной памяти) от всех остальных команд.

Любой алгоритм, работающий по принципу транзитивного замыкания, поддерживает два множества вершин соответствующего графа: множество А активных вершин и множество Р пройденных вершин. Множество Р сначала пусто и в дальнейшем только пополняется. Множество А вначале включает начальные вершины, при шаге обработки отдает обработанные вершины множеству Р и пополняется непосредственными преемниками обрабатываемой вершины. В ЯР-автопроекторе эти множества являются подмножествами прямого произведения множества меток обрабатываемой программы на множество состояний доступной памяти. Элемент этого прямого произведения соответствует данной команде, выполняемой на данном состоянии доступной памяти.

Остальные пояснения будут сделаны в виде примечаний к отдельным командам программы, занумерованным в 16-ричной системе.

Аргументами ЯР-автопроектора являются вектор П[М] входной программы, где М — множество меток ее команд, а также величина Пвход, равная метке входа. Загрузка заданной памяти считается сделанной до начала работы автопроектора. Указание разбиения величин входной программы на заданную, доступную и задержанную памяти производится в виде настройки элементарных синтаксических предикатов, выделяющих величины обрабатываемой программы и узнающих среди них указанные три сорта памяти.

Команда 0. Инициализация. Множество активных состояний содержит элемент, соответствующий тому факту, что начальная команда обрабатываемой программы выполняется на незаданной доступной памяти (ω — условное обозначение полностью неопределенного состояния памяти).

Команда 1. Обращение к служебной процедуре ШАГ. Множества А и Р являются и аргументами, и результатами процедуры, величина а (результат) принимает значения элементов множества А, а также особое значение пуст. Если множество активных состояний пусто, то а получает значение пуст. Если А непусто, то из него изымаются элементы до тех пор, пока не будет обнаружен элемент, не принадлежащий множеству пройденных состояний Р. Этот элемент присваивается величине а в качестве очередного активного состояния, а также пополняет множество Р.

Команда 2. Завершает работу автопроектора при опустошении множества активных состояний.

Команда 3. Величина СОСТ принимает значение текущего состояния доступной памяти. Как указывалось выше, остаточная программа получается редукцией исходной программы, размноженной в количестве экземпляров, равном числу состояний доступной памяти. Если считать, что обрабатываемая программа образует вертикальный столбец, то размноженная программа имеет вид матрицы, где столбец соответствует некоторому состоянию доступной памяти. Каждая команда (элемент матрицы) имеет в качестве метки текстуальное представление координат этого элемента (метка команды, состояние доступной памяти), т. е. как раз значение текущего элемента множества активных состояний (величина а). Обработка текущего активного состояния приводит к построению соответствующей команды остаточной программы. Формирование команды происходит путем конкатенаций текста, выдаваемого командой печати. Аргумент команды печати — это конкатенация конкретных литеральных констант (взятых в кавычки) и значений литеральных переменных и выражений. Операция конкатенации знака не имеет. Печать в команде 3 текстуально представляет значения величины а и вслед за ним двоеточие, т. е. метку еще не построенной очередной команды остаточной программы.

Команда 4. Величина МЕТ принимает значение метки очередной команды обрабатываемой программы.

Команда 5. По значению синтаксического предиката новсост (новое состояние) разделяются два варианта построения очередной команды остаточной программы: случай, когда соответствующая команда обрабатываемой программы вырабатывает новое состояние доступной памяти (команды 6, 7), и случай прочей команды, не меняющей состояния доступной памяти (команды 8, 9).

Команда 6. Формируемая команда остаточной программы имеет пустое действие, поскольку действие соответствующей команды обрабатываемой программы (изменение состояния доступной памяти) отрабатывается в процессе смешанных вычислений. Таким образом, остается лишь сформировать именующее выражение команды, определяющее преемников построенной команды. Поскольку все метки остаточной программы — это пары (метка команды из обрабатываемой программы, состояние доступной памяти), то именующее выражение является конкатенацией двух выражений: первое выдает метку из обрабатываемой программы, второе — выдает новое состояние доступной памяти.

Оба выражения, входящие в команду остаточной программы, получаются из исходных применением базовой операции РЕД(С, Е). Эта операция осуществляет редукцию выражения Е на состоянии доступной памяти С. В первом члене редуцируется именующее выражение команды обрабатываемой программы, во втором члене редуцируется выражение, по которому вычисляется новое состояние доступной памяти.

Команда 7. В этой команде используется еще одна базовая операция ВОЗМ(С, Е), которая выдает множество возможных состояний доступной памяти при вычислении выражения Е на состоянии С доступной памяти. Эта операция создает множество состояний (а не только одно значение), потому что в выражение Е могут входить задержанные вершины, не позволяющие редуцировать Е к константе. В то же время для анализаторных программ постулируется, что влияние задержанных величин на выражения, перевычисляющие состояние доступной памяти, ограничено и сводится к выбору одного из заранее известного множества состояний, выдаваемого операцией ВОЗМ.

Команда 8. Строит команду остаточной программы, не меняющую состояние доступной памяти. Печатается действие исходной команды обрабатываемой программы, выражения которого редуцируются на текущем состоянии доступной памяти с помощью базовой операции РЕДОП (редукция оператора). Вслед за редуцированным действием помещается именующее выражение для преемника, которое является конкатенацией редуцированного именующего выражения из команды обрабатываемой программы с неизменным текущим состоянием.

Команда 9. Загружает переменную S неизменным текущим состоянием доступной памяти.

Команда А. Завершает обработку текущего активного состояния, пополняя множество активных состояний А метками возможных преемников построенной команды остаточной программы. Это пополнение находится как прямое произведение множества возможных значений именующего выражения исходной команды обрабатываемой программы на текущем состоянии доступной памяти (находится с помощью базовой операции ВОЗМЕТ — возможные метки) и множества возможных новых состояний доступной памяти, заданного значением величины S.

§ 2. Генерирующее расширение

Построенный автопроектор, невзирая на его кажущуюся простоту, обладает большой «разрешающей способностью», кратко рассматривавшейся в [10]. Мы проведем дальнейшее обсуждение его возможностей в следующем разделе, а пока заметим, что решающим тестом эффективности автопроектора является нахождение его проекции на самого себя (проекция F3). Результирующая ЯР-программа показана на рис. 2. В ЯР-автопроекторе заданной памятью является обрабатываемая программа П и метка ее начала Пвход. Единственной доступной величиной является переменная МЕТ. Если П загружается программой автопроектора, то очевидно, что множеством всех возможных состояний допустимой памяти будут метки 0, 1, …, 9, А, В. Тем самым остаточная программа расположится в пределах матрицы П[i, j] порядка 12 x13 (с учетом «значения» ω).

Программа (рис. 2) приведена в сокращенном виде. Полная структура получается при расписывании каждого элемента матрицы П[i,j] с подстановкой конкретных значений индексов.

Для тех, кто пожелает воспроизвести проекцию F3, отметим специфические свойства редукций РЕДОП и РЕД (на примере функции РЕД(S, E)):

а) РЕД прогрессирует, если S задано и E содержит переменные, входящие в состояние S. В этом случае такие переменные в E заменяются на их значения, заданные состоянием S;

б) РЕД задерживается, если S задержано и E содержит входные переменные и переменные, входящие в состояние S;

в) РЕД применяется и выдает либо редуцированное E, если оно содержит операции с константными аргументами, либо неизменное, если E информационно не связано с переменными, входящими в состояние S.

Из [5] известно, что проекция автопроектора на самого себя, примененная к программе P(x, y), работает как построитель G ее генерирующего расширения G(P), удовлетворяющего свойству

G(P)(a, y) = P_a(y).

В этой же работе [5] было приведено генерирующее расширение программы возведения x в степень N для случая x задержанного и n доступного. В обозначениях языка реализации программа имеет вид

Входная переменная N, доступная память n, задержанные y, x:

начало: n:= N на иниц
иниц: у := 1 на цикл
цикл: на если n > 0 то тело иначе все
тело: на если нечет (n) то yx иначе xx
ух: у := у × х на вычит
вычит: n := n — 1 на хх
хх: х := х × х на деление
деление: n := n/2 на цикл
все: стоп на ω

П[0,ω ]: А:={(Пвход, ω)}; Р := Ø на 1 ω
П[1,i ]: ШАГ(А, Р, а) на 2i (i = ω, 0, …, B)
П[2,i ]: на если а = пуст то Bi иначе 3i (i = ω, 0, …, В)
П[3,i ]: СОСТ := сост из а; печать (":") на 4i (i = ω,0,…,D)
П[4,i ]: на 5 метка из а
П[5,i ]: на 8j (j = 0, …, 3, 5, …, B)
П[5,4 ]: на 64
П[6,4 ]: печать ("на 5 метка из а) на 74
П[7,4 ]: S := ВОЗМ(СОСТ, "метка из а") на А4
П[8,0 ]: печать (РЕДОП(СОСТ, "А:={(Пвход, ω)}; Р:= Ø")
"на 1" СОСТ) на 90
П[8,1 ]: печать ("ШАГ(А,Р,а) на 2" СОСТ) на 91
П[8,2 ]: печать ("на если а = пуст то В иначе 3" СОСТ) на 92
П[8,3 ]: печать ("СОСТ:= сост из а; печать (а":") на 4" СОСТ) на 93
П[8,5 ]: печать ("на" РЕД (СОСТ, "если новсост(МЕТ) то 6 иначе 8")
СОСТ)на 95
П[8,6 ]: печать (РЕДОП(СОСТ, "печать "на"
РЕД(СОСТ, преемник из П[МЕТ]) П[МЕТ]))") "на 7" СОСТ) на 96
П[8,7 ]: печать (РЕДОП(СОСТ, "S:= ВОЗМ(СОСТ, источник из П[МЕТ])")
"на А" СОСТ) на 97
П[8,8 ]: печать (РЕДОП(СОСТ, "печать (РЕДОП(СОСТ, действие из
П[МЕТ]) "на" РЕД(СОСТ, преемник из П[МЕТ]СОСТ")
"на 9" СОСТ) на 98
П[8,9 ]: печать ("S:= {СОСТ} на А" СОСТ) на 99
П[8,А ]: печать (РЕДОП (СОСТ, "А:= А ВОЗМЕТ(СОСТ, преемник из
П[МЕТ])×S ") "на 1" СОСТ) на 9А
П[8,В ]: печать ("стоп на ω" СОСТ) на 9В
П[9,i ]: S := {СОСТ}на Аi (i = 0, …, В)
П[А,0 ]: A := A {1} × S на 10
П[А,1 ]: A := A {2} × S на 11
П[А,2 ]: A := A {3, В} × S на 12
П[А,3 ]: A := A {4} × S на 13
П[А,4 ]: A := A {5} × S на 14
П[А,5 ]: A := A ВОЗМЕТ(СОСТ, "если новсост(МЕТ) то 6 иначе 8") × S на 15
П[А,6 ]: A := A {7} × S на 16
П[А,7 ]: A := A {А} × S на 17
П[А,8 ]: A := А {9} × S на 18
П[А,9 ]: A := A {А} × S на 19
П[А,A ]:A := A {1} × S на 1А
П[А,B ]:A := A Ø × S на 1В
П[В,i ]: стоп на ωi (i = ω, 0, …, В)

Рис. 2. Генерирующий расширитель (cocom) в языке реализации.

Генерирующее расширение программы (отредактированное в соответствии с требованиями языка реализации) согласно [5] имеет вид

начало: n := N на нач-мет
нач-мет: МЕТ: = 'm0' на иниц
иниц: печать (МЕТ " у := 1 на" след(МЕТ)) на след-иниц
след-иниц: МЕТ:= след(МЕТ) на цикл
цикл: на если n > 0 то тело иначе все
тело: на если нечет(n) то ух иначе хх
ух: печать (МЕТ ": у := у × х на" след(МЕТ)) на след-ух
след-ух: МЕТ := след(МЕТ) на вычит
вычит: n := n — 1 на хх
хх: печать(МЕТ ": х := х × х на" след(МЕТ)) на след-хх
след-хх: МЕТ := след(МЕТ) на деление
деление: n := n/2 на цикл
все: печать (МЕТ ":стоп на ω") на след-все
след-все: стоп на ω

Здесь МЕТ — литеральная переменная, хранящая текущую генерируемую метку, поступающую в остаточную программу, след(МЕТ) — генератор новой текущей метки.

Генерирующее расширение возведения x в степень n, полученное с помощью программы cocom с рис. 2, показано на рис. 3.

При N = 5 оба генерирующих расширения выдают одинаковые (с точностью до выбора имен) остаточные программы:

Согласно [5]	Согласно данной работе (после устранения транзитивных переходов с пустым действием)
m0: y := 1 на m1	иниц5: у := 1 на ух5
m1: у := у × х на m2	ух5: у := у × х на хх4
m2: х := х × х на m3	хх4: х := х × х на хх2
m3: х := х × х на m4	хх2: х := х × х на ух1
m4: у := у × х на m5	ух1: у := у × х на хх0
m5: х := х × х на m6	хх0: х := х × х на все 0
m6: стоп на ω	все0: стоп на ω

Сделаем ряд сравнительных замечаний к рассмотренным двум вариантам генерирующего расширителя на примере программы возведения в степень (назовем их по годам описания G-77 и G-86).

Генерирующие расширители имеют разные механизмы порождения меток остаточной программы. В G-77 генерация меток синхронизована печатью команд остаточной программы, образуя одномерную последовательность. В G-86 метка остаточной программы «вычисляется» на состоянии доступной памяти, а общий вид метки отражает «матричное» строение остаточной программы.

увеличить

В G-77 управление выполнением исходной программы полностью сохраняется в ее генерирующем расширении. Если исходная программа зацикливается на заданной памяти, то то же произойдет при исполнении ее генерирующего расширения. В G-86 генерирующее расширение завершается всегда (если только область значений доступной памяти действительно конечна). За это приходится расплачиваться сохранением в генерирующем расширении механизма нахождения транзитивного замыкания — поддержания множеств A и P. Можно, однако, избавиться от избыточного недетерминизма в процедуре ШАГ, размещая элементы множества A в структурной памяти (стек, очередь) с некоторой детерминированной процедурой занесения и выборки.

§ 3. Анализ

Ниже мы кратко обсудим возможные ответы на 10 вопросов, поставленных во введении. На некоторые вопросы мы отвечаем, опираясь на другие исследования или общие соображения, однако основу анализа образуют разные эксперименты, выполненные с автопроектором из § 1 и генерирующим расширителем (транслятором трансляторов) из § 2.

1. Откуда берутся фазы трансляции? Исходная идея проста. Пусть проецируемая программа P имеет факторизованную область данных в виде трех независимых переменных: P = P(Х1, Х2, Х3). Тогда обработка такой программы смешанным вычислителем M естественно факторизуется на три фазы:

1-я фаза 2-я фаза Исполнение

Такое фазирование, однако, не соответствует интуитивному представлению о декомпозиции транслятора на последовательно применяемые блоки. При таком подходе декомпозиция программы P происходит одновременно с обработкой конкретных значений переменных Х1, Х2, и Х3, т. е. реализуется эквивалентность P(x1, x2, x3) = M(M(P, x1), x2)(x3).

Нас же интересует поиск оператора F, который обеспечивал бы следующее соотношение: F: P(Х1, Х2, Х3) → Р3(Х3, Р2(Х2, Р1(Х1))), при этом Р(х1, х2, х3) = Р3(х3, Р2(х2, Р1(х1))).

Нам не удалось пока найти общего выражения оператора F через оператор смешанных вычислений.

Некоторый намек на направление поисков подсказывают следующие два модельных примера.

Пример 1. Пусть программа P имеет вид

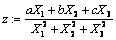Интуитивное представление о фазировании подсказывает следующий вид компонент Р1, Р2, Р3:

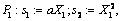
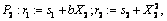
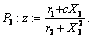
Оператор, выполняющий такое преобразование, хорошо известен в системном программировании: это оператор последовательной декомпозиции. Его выражение, похоже, требует универсальной процедуры, которую условно можно было бы назвать симметризованным генерирующим расширителем. Обычный генерирующий расширитель разбивает текст программы на исполняемую часть и отторгаемую часть, которая при исполнении генерирующего расширения выдается в качестве остаточной программы. При этом исполняемая и отторгаемая части находятся, так сказать, на разных уровнях, последняя — в виде аргументов команд печати текста остаточной программы.

Симметризованный генерирующий расширитель должен «отторгаемую» (2-ю фазу) и «исполняемую» (1-ю фазу) части представить каждую в скомпонованном виде, обеспечив движение информации и передачу управления от первой фазы ко второй.

Пример 2. Введем формальное усложнение в программу xN, состоящее во введении промежуточной величины a, полагаемой ист или ложь в зависимости от нечетности или четности текущего значения величины n. Последовательные значения a, выстроенные справа налево, образуют двоичное разложение N:

начало:   n := N на иниц
иниц:   у := 1 на цикл
цикл:   на если n > 0 то тело иначе все
тело:   а := нечет(n) на нечет
       нечет:   на если а то ух иначе хх
      ух:   у := у × х на вычит
      вычит:   n := n − 1 на хх
      хх:   х := х × х на деление
деление:   n := n/2 на цикл
     все:   стоп на ω

Зададимся теперь целью — разбить алгоритм на две фазы: 1) получение двоичного разложения и 2) использование полученного разложения. Естественным представляется следующее расчленение:

ФАЗА 1: n := N на иниц
   иниц:   m := 0 на цикл
    цикл:   на если n > 0 то тело иначе ФАЗА2
     тело:   m := m + 1 на тело 1
тело 1:   a[m] := нечет(n) на нечет
   нечет:   на если a[m] то вычит иначе деление
вычит:   n := n — 1 на деление
     деление:   n := n/2 на цикл
      ФАЗА2:   у := 1 на начало
       начало:   k := 0 на счет
      счет:   если m > k то работа иначе все
       работа:   k := k + 1 на проверка
проверка:   на если а[k] то ух иначе хх
ух:   у := у × х на хх
хх:   х := х × х на счет
все:   стоп на ω

Этот пример близок к задаче выделения из трансляции фазы разбора (если полагать N входной программой, а вектор a — ее разбором). Пример демонстрирует в дополнение к предыдущему еще одну возникающую при декомпозиции задачу: векторизацию последовательности промежуточных результатов. На первый взгляд, решение этой задачи требует чисто содержательного подхода. Похоже, что решение задачи векторизации может быть регуляризовано для случая анализаторных программ, где векторизация возникает естественно при рассмотрении всех состояний доступной памяти, на которых в данном случае вычисляются значения переменной a.

2. Фундаментальность однопросмотровой схемы. Анализ первого вопроса приводит к заключению, что транслятор, получаемый как генерирующее расширение интерпретатора, является формально однопросмотровым, поскольку его фазирование требует дополнительных механизмов.

3. Специфические механизмы однопросмотровой схемы. Однопросмотровая схема трансляции в ее классическом выражении требует однократного прочтения входной программы и однократной генерации объектного кода. Выполнение этих требований приводит к некоторым специфическим механизмам адресации команд и величин. Например, нельзя напрямую заменить метку в команде перехода на адрес, так как команда, помеченная данной меткой, еще не достигнута и адрес ее неизвестен.

Возникает вопрос: что является эквивалентом этих специфических механизмов в смешанном вычислителе?

Анализ показывает отсутствие единого ответа на этот вопрос, и вид конкретного механизма адресации в трансляторе, получаемом с помощью смешанных вычислений, определяется несколькими факторами.

Во-первых, модифицируется само представление о просмотре. В классических схемах однопросмотровой трансляции работа управляется «слепым» — строго слева направо — перебором входной строки. Просмотр в смешанных вычислениях является просмотром команд интерпретатора при попытке их выполнить, используя элементы входной строки в качестве аргументов этих команд. Такая модификация понятия просмотра снимает часть проблем, хотя и создает новые — в принципе, входная строка должна обрабатываться в режиме прямого доступа к ее элементам.

Во-вторых, некоторые по виду специфические приемы трансляции на деле имеют свои корни в особенностях функционирования интерпретатора и лишь переносятся в транслятор смешанным вычислителем.

В-третьих, и это главное, конкретный вопрос адресации объектов входного языка в объектном коде в случае класса анализаторных программ решается «автоматически» благодаря механизму размножения проецируемой программы над множеством состояний допустимой памяти.

Продемонстрируем действие этого механизма на задаче трансляции переходов по метке.

Пусть во входной строке есть следующие фрагменты:

на L … на M … на L … L: K1 … M: K2.

Очевидно, что интерпретатор имеет среди своих величин переменную, скажем, очереднаякоманда, принимаемую в качестве своих значений информацию о положении очередной команды во входной строке, например, в виде метки. Тогда обработка первого фрагмента на L будет состоять в присваивании L величине очереднаякоманда и к передаче управления (goto) на цикл обработки очередной команды интерпретатором, скажем, по метке NEXT.

Переменная очереднаякоманда относится к допустимой памяти, поэтому смешанный вычислитель занесет во множество активных состояний пару (NEXT, L) (о существовании других допустимых величин можно пока забыть). Аналогично при обработке фрагмента на M во множество активных состояний будет занесена пара (NEXT, M). При этом если переходы на L и на M во входной программе управляются данными входной программы, то обработка этих команд интерпретатором будет задержана и, стало быть, переходы в интерпретаторе на метку NEXT будут перенесены в остаточную программу, но в виде goto (NEXT, L) и goto (NEXT, M).

При достижении интерпретатором фрагмента L: K1 (т. е. при выборке из множества активных элементов пары (NEXT, L)) смешанный вычислитель будет проецировать, начиная с команды NEXT, интерпретатор при состоянии доступной памяти (L). Использование этой информации приведет к тому, что вслед за меткой остаточной программы (NEXT, L) будет размещаться проекция интерпретатора на команду K1, т. е. ее объектный код ob(K1). Аналогично будет обработан и фрагмент M: K2. Таким образом, в результате просмотра указанной входной строки в остаточной программе можно будет найти следующие фрагменты:

goto (NEXT, L) … goto (NEXT, M) … goto (NEXT, L)
… (NEXT, L): ob(K1) … (NEXT, M) : ob(K2)

4. Шаблоны объектных конструкций. Шаблоны объектных конструкций — это заголовки объектных команд, которые в нужном порядке ставятся в объектную программу. В этих шаблонах есть занумерованные пустые места, своего рода формальные параметры, которые замещаются именами величин объектной программы.

При получении транслятора с помощью генерирующего расширителя (процедура cocom) роль шаблонов объектных конструкций играют нередуцированные остатки интерпретатора, отторгаемые в остаточную программу командами печати. Литеральные переменные, погруженные в эти остаточные конструкции, играют роль формальных параметров, замещаемых именами данных входной программы или же сопоставленными этим именам объектами, порожденными интерпретатором (например, машинные адреса).

5. Таблица символов. Уровень абстракции смешанного вычислителя, показанного в этой работе, слишком высок, чтобы точно обозначить место появления таблицы символов. Она может появиться как компонент, уже встроенный в интерпретатор, например, чтобы поддерживать соответствие между именами и ячейками памяти, или же как конструкция смешанного вычислителя, поддерживающая множество состояний допустимой памяти.

6. Стек в трансляторе. Ситуация со стеком аналогична вопросу о таблице символов. Нами был исследован вопрос о судьбе стека, встроенного в интерпретатор. Смешанные вычисления безошибочно вычисляют все действия со стеком, которые могут быть отработаны на периоде трансляции, оставляя в остаточной программе только операции периода исполнения. Представляет не меньший интерес еще не проведенное исследование встраивания стека в смешанный вычислитель для поддержки множества активных элементов. Это, похоже, поможет существенно повысить степень универсализации манипуляций со стеком при построении трансляторов.

7 и 9. Получение транслятора из денотационной семантики. Для входного языка МИЛАН [5] нами были построены в языке реализации два варианта исполняемой семантики: одна — чисто операционная в виде одноциклового интерпретатора, а другая имитировала денотационную семантику в виде системы рекурсивных процедур. В дополнение к этому в языке реализации был реализован стековый механизм исполнения рекурсивных процедур. В результате были получены два очень непохожих интерпретатора, продуцирующих, к большому нашему удовлетворению, идентичный (с точностью до обозначений) объектный код.

Что касается трансформационной семантики, то такого конкретного эксперимента еще никто не делал. Легко показать, что трансформационная семантика, рассматриваемая как рекурсивное определение отображения TS: (P × D) → (P × D) (P — программа, D — данные), описывается сходно с денотационной DS: (P × D) → D. Это сходство вселяет оптимизм в выполнимости такого рода эксперимента.

8. Источники операциональности транслятора. Этот вопрос весьма важен методологически, так как указывает, куда предпочтительнее вкладывать технологический капитал: в смешанный вычислитель или в интерпретатор входного языка. Нам представляется, что для ответа на этот вопрос лучше всего рассматривать транслятор как генерирующее расширение интерпретатора. В генерирующем расширении можно усмотреть компоненты типов:

исполняемую часть исходной программы;
отторгаемую часть исходной программы (в виде литеральных аргументов команд печати);
команды печати (команды генерации);
команды организации информационной связи между исполняемой и отторгаемой частями программы. Это, прежде всего, процедура редукции;
общую организацию генерирующего расширения (ведение множества активных и пройденных элементов).

Первая часть — это прямой вклад интерпретатора в транслятор (прежде всего, лексический и синтаксический анализы). В то же время введение промежуточных имен при декомпозиции существенно зависит от процедур редукции (вклад смешанного вычислителя).

Вторая часть к операциональности транслятора прямого отношения не имеет, хотя на ней фокусируется искусство записи интерпретатора и «разрешающая сила» смешанного вычислителя.

Остальные части — это прямой вклад смешанного вычислителя.

10. Семантические инварианты языка. Сейчас еще преждевременно отвечать на этот вопрос. Мы верим, что систематическое построение транслятора методом смешанных вычислений позволяет гарантировать корректность трансляции при заданной семантике языка либо, наоборот, проверить корректность нового способа задания семантики, требуя идентичного объектного кода при разных семантиках языка. При таком подходе мы берем в качестве инварианта семантик объектный код входной программы.

Однако это только одна сторона проблемы. Развитый транслятор имеет разнообразные средства оптимизации. Значительная часть классических видов оптимизации поглощается смешанными вычислениями (прежде всего, все виды редукционной оптимизации). Комбинаторная же оптимизация — это независимое измерение в обработке программ. Она, прежде всего, связана не с семантиками входного языка, а с семантикой инструментального языка, языка реализации. Здесь мы имеем дело с другими, схемными инвариантами программы.

Стыковка этих двух аспектов семантики транслируемой программы — дело будущего.

Заключение

Сделанный анализ носит сугубо предварительный характер. Тем не менее, даже самые поверхностные наблюдения подтверждают плодотворность изучения проблемы трансляции на основе смешанных вычислений. В свою очередь, смешанные вычисления на классе анализаторных программ позволяют не только получать принципиальное решение задачи трансляции, но и добиваться получения конкурентноспособных схем трансляции. Движение в этом направлении, однако, требует интенсивных экспериментов и решения большого количества технологических проблем.

Список литературы

ERSHOV A. P. On mixed computation: informal account of the strict and polyvariant computation schemes. — In: M. Broy (Ed.) Control flow and data flow: concepts of distributed programming. Berlin a.o.: Springer-Verlag, 1985, S. 107—120.
FUTАMURA Y. Partial evaluation of computation process — an approach to a compiler-compiler. — Systems-Computers-Controls, 1971, v. 2, N 5, p. 45—50.
ЕРШОВ А. П. Об одном теоретическом принципе системного программирования. — Докл. АН СССР, 1977, т. 233, № 2, с. 272—275.
TURCHIN V. F. A supercompiler system based on the language REFAL. — SIGPLAN Notices, 1979, v. 14, N 2, p. 46—54.
ЕРШОВ А. П. О сущности трансляции. — Программирование. 1977, № 5, с. 24—39.
BROOKER R. A., MacCALLUM I. R., MORRIS D., ROHL J. Z. The Compiler Compiler. Annual Review in Automatic Programming. v. 3. London: Pergamon, 1963.
MAZAHER S. An approach to compiler correctness. Ph.D. Dissertation, Computer Science Department, University of California in Los Angeles, 1981.
MAZAHER S., BERRY D. M. Deriving a compiler from an operational semantics written in VDL. — Computer Languages, 1985, v. 10, N 2, p. 147—164.
JONES N. D., SESTOFT P., SONDERGAARD H. An experiment in partial evaluation: the generation of a compiler generator. — In: Proc. 1st Intl. Conf. on rewriting techniques and application. Dijon, France, 1985. Lecture Notes in Computer Science. V. 202. Berlin a.o.: Springer, 1985, p. 124—140.
БУЛЬОНКОВ М. А. Смешанные вычисления для программ над конечно-определенной памятью с жестким разбиением. — Докл. АН СССР, 1985, т. 285, с. 1033—1037.
ERSHOV A. P., ITKIN V. E. Correctness of the mixed computation in Algol-like programs. — In: Mathematical foundation of computer science. J. Gruska (ed.) Lecture Notes in Computer Science, V. 53. Berlin a.o.: Springer, 1977, p. 59—77.

Примечание

[1] Напечатано в сборнике «Прикладная логика (Вычислительные системы, 116)». Новосибирск, ИМ СО АН СССР, 1986.

[2] Ёсихико Футамура (р. 1942) — японский математик, специалист в области методологии программирования и автоматической генерации программ. Сотрудник исследовательской лаборатории Hitachi (1965—1991), профессор факультета информации и вычислительных наук университета Васеда (1991—2005); в настоящее время — президент и руководитель Института Футамуры.

[3]Валентин Федорович Турчин (р. 1931) — советский математик, философ, публицист-диссидент; автор алгоритмического языка РЕФАЛ. С 1977 г. живет и работает в США: 1977—1979 — сотрудник Курантовского института, с 1979 года — профессор на кафедре вычислительной математики в City College Нью-Йоркского университета.

Из сборника «Андрей Петрович Ершов — ученый и человек». Новосибирск, 2006 г.
Перепечатываются с разрешения редакции.