Alexander Andreevich Samarskiy

Home → Hall of Fame → Alexander Andreevich Samarskiy

Mathematician – Academician of the Russian Academy of Sciences

Edition and translation: Alexander Nitusov

Alexander Samarskiy – world famous scientist, founder of the Soviet school of mathematical modelling. Samarskiy is the author of the operator-differential schemata theory and general theory of the schemata stability. He also notably contributed to development of computer-oriented applied numerical methods of mathematical physics.

Alexander Samarskiy was born on the 19 th of February 1919 into a peasant family with many children, in settlement New Ivanovskoe near Donetsk ( South-East Ukraine ). At the age of 14 Samarskiy moved to university town of Taganrog (South-West Russia ) where he entered good secondary school (named after writer and playwright A.P. Chekhov). In 1936 he graduated from it with excellent results (with a Gold Medal) and than had a difficult choice to make, namely what university to enter, whether the famous (Moscow) Institute of Philosophy, Literature and History (IPhLH) or -not less famous- Physical faculty of the Moscow State University (MSU).

The MSU finally “enjoyed the victory”. In 1939 he joined regular scientific seminar of professor A.N. Tikhonov (cooperation of two famous scientists proved to be so fruitful that it lasted many decades after).

In July 1941, with the outbreak of war (World War II) he volunteered to army (same as thousands of other young people) and served in an infantry division formed in Moscow . During the battle of Moscow (winter 1941—1942) he was badly wounded (exploded on a mine when scouting territory controlled by Nazis) and stayed alive literally by miracle. His fellow-soldiers managed to secretly bring him -half dead- in their arms back to the Soviet Army positions and the next ten months he spent in military hospitals of Moscow, Gorkiy (now Nizhny Novgorod on Volga) and finally of Krasnoyarsk and Minusinsk (South Siberia – Altai) thousands kilometres East from Moscow. After (partial) recovery he stayed to work as a teacher at the secondary school in a gold mining settlement “Kommunar” (in the Krasnoyarsk area, North Altai ).

In spite of all wartime difficulties A.N. Tikhonov did not lose connections with his able student. In 1943, much due to his personal efforts, Samarskiy received an official order of the MSU rectorate to return to Moscow for continuing his study at the university. He arrived there still on crotches.

In 1945 Alexander Samarskiy graduated from the physical faculty but continued education as the MSU post-graduate, under Tikhonov's scientific supervision. Despite his young age he was already an experienced, determinate person. That was displayed by his goal-oriented style of work and its impressive results. In parallel with the main subject of his dissertation research he published about 20 various works on quite different physical issues. In 1948 he submitted his dissertation thesis and soon was awarded the “Candidate of Sciences” degree.

In 1957 he was awarded a doctorate. In 1966 Samarskiy was elected a corresponding member of the USSR Academy of Sciences (AS USSR) department of mathematics and ten years later, in 1976, a full academician at the same department.

In 1948 a special laboratory was set up by decision of higher administration. A.N. Tikhonov, then already an academician, was appointed as its director and Samarskiy as his leading assistant. They jointly started development of numerical methods and then conducted the USSR first direct calculations on atomic explosion power. They implemented mathematical models describing dynamic of gases motion, transference of warmth and neutrons, emission of energy and many other complex processes. Later the same calculations were repeated for a hydrogen bomb. The both theoretical results perfectly coincided with experimental data. Those works already incorporated foundations of mathematical modelling and also introduced principles of composing and proving differential schemas as basis for numerical methods. In 1958—1960, basic results of the research were being published by Samarskiy and Tikhonov in academic periodicals Doklady AN SSSR .

In 1960-s obvious success of his theoretical works and solid experience in solution of applied problems permitted him and his collaborators to essentially extend range of their research and set up new research programs on thermo-nuclear laser synthesis, development lasers of increased power, radiation and magnetic dynamics of gases, magnetic hydro-dynamics, nuclear power production, physics of plasma, continuum mechanics and even aerodynamics. Most of those subjects were previously inaccessible with traditional methods for their complexity and non-linearity.

Progress of those works had decisive and clear influence on forming of methodology in mathematical modelling and computational experimenting. It is famous as “Samarskiy's triad” – model-algorithm-program .

Thus methodology of mathematical modelling eventually received a “Citizenship”. Officially registered discovery of, so-called, T-layer, first by the mathematical experiment and only then by traditional physical experiment could be a good prove of that.

Natural need in proving applied calculations by the usage of computers (his article dedicated to the issue was called, “Inevitability of new Methodology”) led Samarskiy to the idea of operator theory of differential schemas , which rose much above the world level of that time. He himself referred to the subject as “Intellectual core of information science” and an important factor of forming contemporary information society.

Samarskiy with his collaborators has been actively working in that scientific field. In our days many of their highly efficient algorithms are in intensively used.

He obtained fundamental results in three domains of the theory of differential methods. They are: the theory of network approximation of the mathematical physics' equations , the theory of differential schemas stability and the theory of forming and proving methods of equations solution with the use of differential schemas with higher precession level on non-uniform nets.

The first big cycle of his works on theory of differential methods was focused on solution of stationary problems of mathematical physics. He developed in these researches fundamentals of the theory of uniform differential schemas, and defined a constructive principle of uniform differential schema conservatism in the class of discontinuous coefficients.

The second fundamental cycle of his works was dedicated to differential methods for solving of non-stationary multi-dimensional problems of the mathematical physics. In this cycle he developed method of prior estimations , its implementation enabled estimating of differential schemas convergence speed in various metrics. The principle of integrated approximation, which was also suggested in that research, formed the basis for creation of rational differential solution schemas of both linear and non-linear equations in mathematical physics.

One more cycle of his researches was titled, “Stability Problems in general Theory of Differential Schemas”. It mainly dealt with theory of two- and three-layer differential schemas stability. Both types of schemas were considered as operator-differential equations within Hilbertian Space.

Basic achievements of his stability theory consisted in introduction of unified canonical form of differential schemas notation and in obtaining of necessary and sufficient criteria of stability in terms of operator inequalities .

Thus for the two-layer differential schema

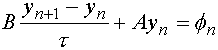
n=1,2,… (A, B – limited linear operators in Hilbertian space) there is a necessary and sufficient condition of stability, which is represented with classical matrix inequality B-0,5 t A>=0 .

Emergence of Samarskiy's stability theory made possible efficient estimation of iteration processes convergence degree and definition of optimal values of iteration parameters necessary for practical development of applied programs.

Spacious range of Samarskiy's works on mathematical physics and differential equations also incorporate big domain oriented on theory of non-linear equations in mathematical physics. He proposed new analytical and numerical research methods for non-linear stage of processes developing in a blow-up mode. His researches proved predictions on new phenomena in plasma physics and in localisation of diffusion processes. They also brought new original results in studying of diffusion chaos phenomenon.

Besides impressive scientific researches he also ‘paid tribute' to organisational activity. In 1986—1987 he headed development of National Program on implementation methods of mathematical modelling in science and economy. In the same 1986 he arranged administrative backing up for the program by establishing All-Union Centre for mathematical modelling.

From 1953 till 1991 Samarskiy held a department at the M.V. Keldysh Institute of Applied Mathematics (AS USSR), in 1990 he transformed the All-Union Centre into the Institute of Mathematical Modelling (at the AS USSR/RAS) and was its director until 1998.

At present he is a scientific head of this institute and a councillor of RAS.

Samarskiy has been lecturing at the MSU since more than 50 years. He set-up and held a chair of computational methods at the famous MSU department (faculty) of computational mathematics and cybernetics and also a chair of mathematical modelling at the Moscow Institute of Physics and Engineering. He personally formed an impressive scientific school; 5 academicians of the AS USSR (RAS) began their careers as his students. Samarskiy supervised dissertation works of more than 40 doctors and 100 candidates of sciences. His -former- students are still working in Germany , Bulgaria , Hungary , Ukraine , Byelorussia , Georgia , Uzbekistan , Azerbaijan , Armenia , Latvia , Lithuania and in USA .

He himself is the honourable doctor (honoris causa) of the universities of Chemnitz ( Germany ), of Tbilissy (Georgia), Taganrog (South Russia) and of the national academies of Byelorussia and Ukraine .

A.A. Samarskiy authored more than 30 monographs and 450 scientific articles. His book “Equations of Mathematical Physics” (A.N. Tikhonov et al.) first appeared in the 1950-s and then was edited several times and translated into 13 foreign languages. It's long since becoming a classical source. Several generations of students and post-graduates studied his books as basic courseware.

He set up academic journal “Mathematical Modelling”, where he is the editor-in-chief and is also working in editorial boards of six Russian and foreign scientific journals. Until now A.A. Samarskiy is the second academic secretary at the Department of Information Sciences, Computer Engineering and Automation RAS. He is the chairman of Russian section of the International Association on implementation of mathematics and computers in modelling (IMACS).

A.A. Samarskiy has been awarded the honourable title “Hero of the Socialist Labour” (one of the highest Soviet civil awards) and is a laureate of the Lenin, State and M.V. Lomonosov premiums. He has been also decorated with orders “Lenin Order” (three times), “Patriotic War“ (1 st Grade), “October Revolution”, “Red Banner of Labour”, “Friendship of the Peoples”, with several medals and other awards.

Sourses:

1. Basic source – “A.A. Samarskiy”, a biography (Russian) in Russian Virtual Computer Museum
2. “Academician Alexander Andreevich Samarskiy (Russ.)” www.imamod.ru
3. foto - http://old.cs.msu.su/vm/samars.htm