Введение в недоопределенность

А.С. Нариньяни

Свойства недоопределенных расширений

В этом разделе мы вернемся к свойствам Н-расширений и обсудим их детальнее.

5.1. Н-математика и субдистрибутивность

Заметим‚ что некоторые свойства обычных операций существенно меняются в соответствующих Н-расширениях. Рассмотрим, например, хорошо известное свойство аддитивных операций над числами (целыми или вещественными), требующее, чтобы сумма любого числа и обратного ему была равна единственному нулевому элементу

a + ( - a) = 0. (1)

Пусть в качестве Н-расширения множества чисел рассматривается Н-расширение интервал [a_-, a^-] , а соответствующие Н-расширения операций минус и плюс (обозначим их -- и ++) определены согласно известным правилам интервальной арифметики [20]. Таким образом, Н-расширение унарного минуса имеет вид

--[ a_- , a^-] = [ - a_- , -a^-];

а Н-расширение сложения [b_- , b^-] ++ [c_- , c^-] равно [ b_- + c_- , b^-+ c^-].

В таком случае, Н-расширение выражения (1) имеет следующий вид:

[a_- , a ^-] ++ (-- [a_-, a^-]) = [a_-, a^-] ++ [-a^-,-a_- ] = [a_- + (-a^-), a^-+ (-a_-)] = [a_- -a^-, a^--a_-].

Достаточно очевидно, что когда нижняя и верхняя границы Н-числа не совпадают (т.е. число недоопределено), интервал [a_- -a^-, a^--a_-] всего лишь содержит ноль, но не равен в точности ему. Например, при а = [2, 4], -а = [-4, -2], -а + а =[-2, 2].

Такое изменение свойства унарного минуса приводит к тому, что закон дистрибутивности для обычных аддитивных и мультипликативных операций переходит в так называемый закон субдистрибутивности ( xx - Н-расширение операции умножения):

*a xx (*b ++ *c) 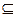*a xx *b ++ *a xx *c.

Из сказанного выше можно сделать вывод, что для Н-моделей весьма существенно:

• какие Н-расширения выбраны для переменных, - например, для целых чисел представления могут быть интервальными или перечислениями;
• в каком виде представлены условия задачи, - над любой системой отношений можно провести множество преобразований, эквивалентных с точки зрения формальной системы, но существенно различных для реализации ее Н-расширения.

Другими словами, для использования Н-модели важно, каким образом представлены в ней и типы Н-переменных и сами ограничения. Например, в какой форме записаны алгебраические зависимости (уравнения и неравенства), т.е. как произведены в них те же самые эквивалентные преобразования - раскрытие скобок, приведение подобных и т.п.

5.2. Проблемы Н-математики

Таким образом, список достоинств рассматриваемого подхода необходимо дополнить указанием на его особенности и недостатки (или, скорее, текущие трудности):

• Как и для любого универсального метода, для Н-моделей во многих (возможно, в большинстве) случаев характерна более низкая эффективность на задачах, для которых существуют специальные вычислительные методы. Хотя есть достаточно примеров, когда аппарат Н-моделей значительно (во ряде случаев, во много раз) превосходит известные алгоритмы. Понятно, что сравнение Н-моделей с известными специальными вычислительными методами на всем спектре прикладных задач требует объема экспериментов, на проведение которых пока нет достаточных ресурсов.
• Вторая особенность состоит в том, что с одной стороны, кроме редких особых - можно сказать, пограничных - случаев, процесс не теряет решений, т.е. процесс стягивания K -мерного пространства модели будет содержать все ее решения . С другой, сам параллелепипед не всегда является минимальным для охватываемой им области решений. Для некоторых задач процесс сжатия может остановиться где-то «на полпути» к минимальному параллелепипеду.
  Чем плотнее параллелепипед охватывает тело решений (чем уже интервалы Н-параметров), тем точнее он представляет это тело для пользователя. В минимальном параллелепипеде концы интервала каждой переменной х являются оптимумами (минимумом и максимумом) проекции на х области решений. Т.е. концы интервала параметра х представляют минимум и максимум решений по х.
  При этом "не дожатый" параллепипед отражает только то, что вне его решений нет. А есть ли решения внутри него вообще и где минимумы и максимумы этих решений, остается неизвестным.
  Для некоторых специальных классов моделей сжатие может вообще не начаться, как это могло бы быть в нашем примере п.3.2, если бы уравнения были симметричными. В частности, таким особым классом являются системы линейных уравнений, хотя после приведения их матрицы к диагональному виду, решение трудностей не вызывает.
• Таким образом, хотя то или иное представление отдельного ограничения, так же как и группы ограничений, будут эквивалентны в традиционной алгебре, однако для Н-моделей при одном представлении полученное в результате стягивания подпространство может быть меньше, т.е. ближе к вложенной в него области решений, а при другом - шире.

В связи с этим, эффективность и универсальность Н-моделей в значительной степени зависит от двух факторов:

(а) Выбора формы символьного представления зависимостей; например, для двух эквивалентных в обычной алгебре выражений

x(6x³ + 1) (4x – 1) = 4 и 24x⁵ + 4x² – x(6x³ + 1) = 4,

сжатие закончится по-разному: первое даст точное решение [0.70574, 0.70574], а второе остановится при стягивании на интервале [0.25072, 3.8939].

Эта особенность требует приведения зависимостей Н-модели к оптимальному для процесса решения виду. Именно поэтому приходится, как уже упоминалось выше, приводить к диагональному виду систему линейных уравнений. Исследования по разработке системы таких оптимизирующих трансформаций ведется достаточно активно.

(б) Не менее важным является выбор представления Н-значения при недоопределенном расширении. Например, целые числа могут представляться интервалом, мультиинтервалом или перечислением значений.

Первый вариант компактней и эффективней, но у него важный недостаток: интервал [а, в] представляет, не различая, любые подмножества значений этого интервала, включающие его границы а и в. Например, решением уравнения 5x² - 3x - 14=0 будет интервал [-2, 2], хотя оно состоящие только из двух значений -2 и 2.

Второй вариант - мультиинтервальный - позволяет исключать часть или все зоны отсутствия решений и в приведенном примере он оставил бы два точных решения или выдал два приближенных к ним интервала. Однако такое представление Н-значения резко замедляет процесс решения.

Наконец, Н-значение, состоящее из списка целых чисел, содержит только те числа, которые могут быть решениями. Однако, при большом диапазоне значений такое представление является слишком громоздким и мало эффективным.

Указанные здесь недостатки и методы их преодоление требуют более развернутого рассмотрения, которое не входило в ограниченные задачи этой вводной работы.

В п. 4.4 мы уже приводили метафору океана реальных задач, на карте которого с развитием технологии ограничений появились очертания целых материков, нечеткость границ которых объясняется коротким сроком разработки этого подхода и относительно небольшим числом его разработчиков. Но соответствующие исследования ведутся активно и достаточно успешно.

Модель vs. алгоритм | Оглавление | Вычислительные Н-модели

Перепечатывается с разрешения автора
Статья помещена в музей 02.10.2008 года