Заметки о троичной цифровой технике - часть 1
Н. П. Брусенцов
Цель этих заметок - охарактеризовать с практической точки зрения особенности и возможности троичной цифровой техники.
Интерес к троичной технике возник уже на начальном этапе развития автоматических цифровых машин в связи с замечательными арифметическими свойствами симметричного кода чисел [1], открытие которых происходило затем снова и снова [2, 3]. Впрочем, имеется мнение [4, с. 81], будто интерес этот обусловлен ошибочным представлением об исключительной экономности троичного кода. Как бы то ни было, но интерес к троичной технике существует, и сама она, хотя и не быстро, но развивается. Укажем, например, что на шести состоявшихся в период с 1971 по 1976 г. симпозиумах по многозначной логике [5] большинство докладов прикладного характера было посвящено троичной технике.
В условиях интегральной технологии и микроэлектроники привлекательность троичной техники увеличивается: сложность трехзначных вентилей теперь не так страшна, а сокращение количества соединений и уменьшение рассеиваемой мощности особенно ценны. Новые преимущества троичного кода выявлены благодаря развитию цифровой связи [6] - области, в которой троичная техника стала использоваться с появлением кабельного телеграфа и успешно применяется в новейших системах. Однако не так важны частные выгоды и преимущества, как гармоничность и эффективность троичной техники в целом, неприсущность ей недостатков и неудобств, свойственных двоичной технике.
Что такое троичная цифровая техника
Современная цифровая техника основана на двузначных сигналах и двухстабильных элементах памяти - это двоичная цифровая техника. Объекты, принимающие более чем два значения, реализуются в ней как совокупности двузначных элементов (битов). Например, десятичные цифры представляются четверками битов, символы алфавита, включаюшего буквы, цифры и некоторые другие знаки, - восьмерками битов (байтами).
Соответственно все операции над недвузначными объектами реализуются как последовательности операций двузначной логики, производимых над битами, совокупностями которых представлены эти объекты. Например, арифметические операции над двоичными числами.
Важными преимуществами двоичной техники, обусловившими ее быстрое развитие и широкое распространение, являются: простота физической реализации битов и операций двузначной логики, некритичность допусков на параметры двузначных сигналов и двухстабильных устройств.
Троичная цифровая техника базируется на трехзначных сигналах и трехстабильных элементах памяти (тритах). Объекты, принимающие более чем три значения, реализуются в ней как совокупности тритов. Операции над этими объектами осуществляются как последовательности операций трехзначной логики. Аналогом байта служит шестерка тритов - трайт. Двузначные объекты и операции над ними содержатся в троичной технике как вырождения тритов и операций трехзначной логики.
Практическая целесообразность троичной техники не очевидна. Ясно, что троичная техника равноценна двоичной технике в том смысле, что все, осуществимое в одной из них, с тем или иным приближением осуществимо и в другой. Ясно также, что трехзначные вентили и элементы памяти должны быть сложнее и дороже, чем двузначные, а трехзначная логика заведомо сложнее двузначной. Но с другой стороны, трехзначные элементы памяти мощнее (трит - это приблизительно 1,585 бита) и операционные возможности трехзначных вентилей богаче. Следовательно, обработка данных в условиях троичной техники осуществляется при одном и том же физическом быстродействии элементов быстрее, а структура троичного устройства, как правило, оказывается проще, чем структура функционально равноценного двоичного устройства. Другими словами, троичная техника характеризуется по сравнению с двоичной усложнением элементов, благодаря которому возможно упрощение создаваемых из них структур и увеличение скорости обработки данных. Замечательно, что троичная техника является единственной недвоичной техникой, не связанной с необходимостью ужесточения действующими в двоичной технике допусков на параметры сигналов и характеристики элементов.
Увеличение значности с двух до трех без ужесточения допусков достигается за счет недоиспользуемой двоичной техникой возможности различать сигнал как по амплитуде, так и по полярности. При этом троичный сигнал x можно рассматривать как суперпозицию его положительной x+ и отрицательной x- двоичных составляющих: x=x+-x-, x+•x-![]() 0. Основанная на таком представлении интерпретация троичной техники как оперирующей не только с троичными сигналами, но и сих положительными и отрицательными двоичными компонентами, которые можно отделять от троичного сигнала, обрабатывать по отдельности и снова соединять в троичный сигнал, позволяет естественно и просто осуществить неформальное построение троичных цифровых устройств [7]. Физически такой подход выражается в том, что вентили, обладающие двоичным выходом положительной полярности, используются совместно с вентилями, обладающими двоичным выходом отрицательной полярности. На входах этих вентилей допустимы сигналы как положительной, так и отрицательной полярности, т. е. применяется трехзначная логика. Выходы положительной и отрицательной полярности можно объединять, благодаря чему в 1,5 - 2 раза увеличивается интенсивность использования соединительных проводов и соответственно сокращается количество соединений между вентилями.
0. Основанная на таком представлении интерпретация троичной техники как оперирующей не только с троичными сигналами, но и сих положительными и отрицательными двоичными компонентами, которые можно отделять от троичного сигнала, обрабатывать по отдельности и снова соединять в троичный сигнал, позволяет естественно и просто осуществить неформальное построение троичных цифровых устройств [7]. Физически такой подход выражается в том, что вентили, обладающие двоичным выходом положительной полярности, используются совместно с вентилями, обладающими двоичным выходом отрицательной полярности. На входах этих вентилей допустимы сигналы как положительной, так и отрицательной полярности, т. е. применяется трехзначная логика. Выходы положительной и отрицательной полярности можно объединять, благодаря чему в 1,5 - 2 раза увеличивается интенсивность использования соединительных проводов и соответственно сокращается количество соединений между вентилями.
Практичность трехзначной логики
Одним из барьеров, сдерживающих развитие и распространение троичной техники, является неверное представление о необычности и трудной постижимости трехзначной логики. Современная формальная логика (как традиционная, так и математическая) основана на принципе двузначности. В числе ее фундаментальных законов имеется закон исключенного третьего: "Третьего не дано", истолковываемый обычно в том смысле, что правильная логика ничего, кроме "Да" и "Нет", допустить не может. Трехзначная логика при этом ассоциируется с интуиционизмом, модальностями, микромиром и другими таинственными вещами, но только не с обыденной действительностью, которая по сложившемуся на протяжении веков убеждению будто бы устроена и функционирует по двоичным правилам. Окутанная подобным научным туманом и характеризуемая, например, тем, что число двухместных функций, равное при двузначных переменных 16, в случае трехзначных переменных составляет 19683 (!), трехзначная логика естественно действует устрашающе.
На самом деле трехзначная логика не только вполне корректна и адекватна действительности, но является даже более удобной и привычной для людей формой мышления, чем двузначная логика. Покажем это. на примерах.
В качестве первого примера рассмотрим рычажные весы (рис. 1), представляющие собой характерное троичное устройство, трем состояниям которого соответствуют три возможных отношения: А>В, А=В, А<В. Для сравнения рассмотрим также двоичные весы, которые могут принимать только два состояния, соответствующие, например, отношениям А>В, А![]() В (рис. 2). Ясно, что двоичные весы существенно менее удобны, чем троичные. Только в случае А>В результат взвешивания на них определяется сразу, а в остальных двух случаях необходимо производить повторное взвешивание, поменяв местами А и В. Практическая работа с такими весами имеет смысл разве как средство переубеждения приверженцев двузначной логики, а с точки зрения других применений их можно рассматривать лишь как испорченные троичные весы. Двоичные цифровые устройства по сравнению с троичными устройствами в отношении логической эффективности занимают примерно такое же положение.
В (рис. 2). Ясно, что двоичные весы существенно менее удобны, чем троичные. Только в случае А>В результат взвешивания на них определяется сразу, а в остальных двух случаях необходимо производить повторное взвешивание, поменяв местами А и В. Практическая работа с такими весами имеет смысл разве как средство переубеждения приверженцев двузначной логики, а с точки зрения других применений их можно рассматривать лишь как испорченные троичные весы. Двоичные цифровые устройства по сравнению с троичными устройствами в отношении логической эффективности занимают примерно такое же положение.
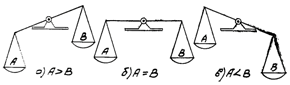
Рис. 1. Троичные весы
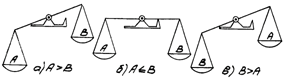
Рис. 2. Двоичные весы
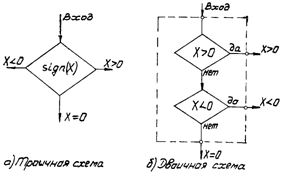
Рис. 3. Ветвление по знаку
Другой пример - ветвление по знаку величины Х (рис.3) - не обладает физической наглядностью примера с весами, но явно демонстрирует принципиальное отличие трехзначной логики от двузначной. Это отличие состоит не в том, что трехзначная логика, как нередко полагают, будто бы позволяет выразить нечто, невыразимое в двузначной логике, а в том, что в точности одно и то же в трехзначной логике может быть выражено более компактно и может быть выполнено за меньшее число шагов. В рассматриваемом примере троичное ветвление по знаку величины Х описано заданием единственной трехзначной операции sign(Х) и выполняется за один шаг, в то время как такое же ветвление, осуществляемое средствами двузначной логики, связано с необходимостью двух операций и выполняется, вообще говоря, за два шага. Нетрудно построить аналогичную схему ветвления в зависимости от отношений, которыми могут быть связаны две величины: Х>У, Х=У, X<Y. В жизни трехзначные отношения, укладывающиеся в данную схему, встречаются очень часто. Например:
увеличить - не изменять - уменьшить, вперед - стой - назад,
выигрывает А - ничья - выигрывает В,
избыток - норма - недостаток,
дружественный - нейтральный - враждебный,
рано - своевременно - поздно,
влево - прямо - вправо
и т. п.
Многие вопросы предполагают тройственный ответ. На это указал еще Аристотель [8]: "Будет ли завтра в полдень морской бой?" - "Да" - "Нет" - "Может быть". Логики утверждают, что этот пример свидетельствует о неприменимости закона исключенного третьего к высказываниям о будущем. Но спросите у вашего соседа, был ли вчера дождь в Батуми. Если только сосед не прилетел из Батуми сегодня утром или не переговорил с кем-то, находящимся в Батуми, по телефону, то ответ его будет ни "Да", ни "Нет", а "Не знаю" или "Может быть". Но ведь высказывается он не о будущем, а о прошедшем! Ясно, что тройственность ответа обусловлена не тем, что вопрос касается будущего, а тем, что ответчик не располагает информацией, необходимой для того, чтобы дать утвердительный или отрицательный ответ. Если в этой, весьма типичной в жизни ситуации ваш сосед окажется двоичным соседом, т. е. таким, который может отвечать только "Да" или "Нет", то во избежание недоразумений Вы должны спрашивать о дожде в Батуми в два приема. Сначала следует спросить, знает ли он о том, был или не был вчера дождь: в Батуми. И только в случае утвердительного ответа на этот вопрос можно спросить, был ли дождь в Батуми.
В обычных разговорах с людьми, конечно, не приходится прибегать к подобным ухищрениям, так как всякий нормальный человек владеет трехзначной формой ответа. Однако в двоичных системах эти ухищрения неизбежны, потому что третье в двузначной логике "не дано".
Например, понятие "бит, значение которого не всегда определено", фактически сводится к тому, что должен быть другой вспомогательный бит, содержащий информацию о том, определено в данный момент значение основного бита или не определено. При этом, поскольку обращение к основному биту имеет смысл только в том случае, когда значение его определено, то всякий раз надо сперва обратиться к вспомогательному биту и лишь затем обращаться к основному, если вспомогательный оказался в состоянии "значение определено".
Приведенные примеры показывают, что трехзначная логика не есть нечто противоестественное или необыкновенное. Она не только доступна для людей, но позволяет рассуждать более просто и более быстро по сравнению с рассуждениями в условиях двузначной логики. На практике люди пользуются, по-видимому, преимущественно трехзначной логикой. Во всяком случае система умозаключений, составляющая логическую основу естественных языков, - силлогистика - построена на принципе трехзначности [9].
Эффективность троичной арифметики
Подобно тому как добавление третьего значения позволяет в значительной мере преодолеть неудобства двузначной логики, введение третьей цифры в систему машинного представления чисел оказывается достаточным для того, чтобы можно было, устранить практически все дефекты двоичной (и десятичной) арифметики. Дело не в том, что число три ближе других целых чисел к основанию натурального логарифма e (хотя усматривать в этом намек на исключительность троичного, конечно, можно), а в том, что три цифры - это минимум, уже позволяющий непосредственно обозначить положительное, отрицательное и нуль. Двоичная система неполноценна в том смысле, что в ней недостает одного из трех этих элементов.
Ради простоты ограничимся рассмотрением целых чисел.
Назовем естественным представлением числа такое представление в позиционной системе счисления с положительным целым основанием p, при котором запись числа в виде ряда цифр а1а2...аn конечной длины n однозначно определяет значение этого числа по формуле
В двоичной системе (p=2) возможно естественное представление либо только неотрицательных (цифры 0 и 1), либо только неположительных (цифры 0 и -1) чисел, либо положительных и отрицательных, но неоднозначное и без нуля (цифры 1 и -1). Практически всегда используют цифру 0 и 1, т. е. естественное представление имеет место только для неотрицательных чисел. Поэтому двоичная арифметика проста и эффективна, пока операции производятся над числами без знака, например, в адресном пространстве двоичной памяти. Заметим, что при этом несложно реализовать выполнение операций с операндами разной длины, поскольку добавление ведущих нулей не изменяет числового значения операнда и, следовательно, может служить средством автоматического выравнивания длин. Если же длина слова фиксирована, то при естественном представлении чисел наиболее просто обнаруживается переполнение сумматора: при переполнении и только при переполнении цифра переноса из старшего разряда сумматора отлична от нуля.
Представление отрицательных чисел в рассматриваемой системе с цифрами 0 и 1 можно получить, производя вычитание большего числа из меньшего. Например, вычитая 1 из 0, имеем где точки означают бесконечное повторение ведущей цифры, обусловленное тем, что имеет место неограниченно распространяющийся влево заем. Таким образом, запись ...111 представляет число -1. Аналогично получим: ...110 для обозначения числа -2, ...101 для -3 и т. д. Замечательно, что при таком представлении отрицательных чисел арифметика, разработанная для двоичных чисел без знака, автоматически распространяется на числа со знаком в том смысле, что алгоритмы выполнения операций над неотрицательным, и числами в естественном представлении остаются в силе при добавлении представленных данным способом отрицательных чисел. Однако, введя точки как символ бесконечного повторения цифры, мы использовали как раз то третье, которого нет в двоичной системе. Пользуясь только цифрами 0 и 1, мы должны явно записывать отрицательные числа словами бесконечной длины. Ведь если просто оборвать распространяющийся влево заем, то отрицательное число нельзя будет отличить от некоторого положительного числа в естественном представлении. Например, отбросив точки в записи ...101 (число -3), получим 101 - положительное число 5.
Впрочем, при фиксированной длине слова можно условиться, что в случае, когда заем отсутствует, первый (левый) бит слова должен содержать цифру 0. Полное представление числа при этом будет получаться просто распространением влево за пределы слова той цифры, которая содержится в его первом бите. Когда число отрицательно, т. е. когда заем имеет место, этой цифрой будет 1, а в случае неотрицательного числа ею будет 0. Обычно говорят, что первая цифра слова является знаком числа, хотя на самом деле она лишь указывает, отрицательно число или нет. Такое предоставление чисел со знаком (называемое дополнительным кодом) не обладает уже преимуществами естественного представления в отношении операций с разной длиной операндов и индикации переполнения, однако является самым употребительным в современных цифровых машинах, потому что позволяет более эффективно, чем другие двоичные коды, реализовать арифметику.
Чтобы показать, насколько троичная арифметика эффективней арифметики, основанной на двоичном дополнительном коде, сопоставим программу, реализующую сложение двух чисел в дополнительном коде на миникомпьютере PDP-8 [10], с программой, осуществляющей равносильную операцию на троичном миникомпьютере, подобном PDP-8 в отношении архитектуры.
Машина PDP-8 обладает 12-битовым аккумулятором Ас (0:11), между крайними битами которого включен однобитовый регистр связи Lk(1: 1). В процессе сложения L14 воспринимает цифру переноса Cr из старшего разряда Ас(0) аккумулятора: Lk:=Lk+Cr. Имеется возможность тестировать Ас и Lk, а также "очищать" их - присваивать значение 0. В кольце LkAc можно производить сдвиг влево: LkAc:= =AcLk и вправо: AcLk: =LkAc.
Сложение чисел в дополнительном коде осуществляется программой, которая использует в качестве слагаемых содержимое ячеек А и В главной памяти, а результат сложения помещает в ячейку SUM. На первом этапе сопоставляются знаки слагаемых и устанавливается одно из трех: 1) знаки противоположны - OPPSGN, 2) оба слагаемые отрицательны - BTHNEG, 3) оба слагаемые положительны - BTHPOS. В каждом из этих случаев сложение выполняется отдельной подпрограммой, причем при переполнении аккумулятора производится переход на POSERR, если слагаемые положительны, и на NEGERR, если отрицательны. Ниже приведен текст программы на языке ассемблера с поясняющими комментариями.
| START, | CLA CLL TAD А AND MASK TAD В SZL JMP BTHNEG RAL SZL CLA JMP OPPSGN JMP BTHPOS |
/Ас: =0; Lk: =0; /Ас: =Ac+A; /Ас (1, 11): = 0; /Ас: =Ac+B; /if Lk=0 /then gо to BTHNEG; /LkAc: =AcLk; /Ас: =0; if Lk=0 /then go to OPPSGN /else go to BTHPOS; |
| OPPSGN, | TAD А TAD В DCA SUM HLT |
/Ас: =Ac+A; /Ас: =Ac+B; /SUM: =Ac; Ас: =0; /STOP; |
| ВТНNEG, | CLA CLL TAD А TAD В SMA JMP NEGERR DCA SUM HLT |
/Ас: =0; Lk: =0; /Ас: = Ac+A; /Ас: =Ac+B; /if not(Ac<0) /then go to NEGERR; /SUM: =Ас; Ас: =0; /STOP; |
| BTHPOS, | TAD А TAD В SPA JMP POSERR DCA SUM HLT |
/Ас: =Ac+A; /Ас: =Ac+B; /if not(Ас>=0) /then go to POSERR; /SUM: =Ас; Ас: =0; /STOP |
| MASK, SUM, А, В, POSERR, |
4000 0 nnnn nnnn ... ... |
|
| NEGERR, | ... ... |
Теперь покажем, как данная процедура может быть реализована в условиях троичной техники. Представим себе троичный вариант процессора PDP-8, т. е. работающую в троичном коде машину с такой же конфигурацией регистров Ас и Lk (заметим, что для обеспечения точности, соответствующей 12 битам, достаточно иметь в аккумуляторе 8 тритов) и аналогичным набором команд. В системе с тремя цифрами можно не получить никаких преимуществ перед двоичной системой, если принять неотрицательные (0, 1, 2) или неположительные (0, -1, -2) значения цифр. Мы используем симметричный набор цифр ( -1, 0, 1), обеспечивающий Однозначное естественное представление всех чисел: положительных, отрицательных и нуля. В этой системе арифметика чисел со знаком так же проста, как арифметика неотрицательных чисел в двоичной системе с цифрами 0, 1. В частности, чтобы обнаружить переполнение аккумулятора, не требуется анализировать знаки слагаемых: признаком переполнения служит ненулевая цифра переноса из старшего разряда в Lk. Если же необходимо не только обнаружить переполнение, но и произвести переход на одну из подпрограмм в зависимости от знака слагаемых, как в рассмотренной выше двоичной программе, то достаточно проанализировать цифру переноса, поскольку она обладает тем же знаком, что и слагаемые.
Анализ цифры в троичной машине естественно выполнять командой трехзначного перескока (пропуска). Такую команду применительно к анализу, Lk мы в духе мнемоники языка ассемблера для PDP-8 обозначим SLS - Skip on Link's Sign. Она предписывает следующую модификацию значения программного счетчика РС:
if Lk=0 then PC:=PC+2 else if Lk=l then РС:=PC+1;
Программа для троичного миникомпьютера, функционально равноценная приведенной выше двоичной программе для PDP-8, состоит из 8 команд:
| START, | CLA CLL TAD А TAD В SLS JMP NEGERR JMP POSERR DCA SUM HLT |
/Ас: =0; Lk: =0; /Ас: =Ac+A; /Ac: =Ac+B; /if Lk= - 1 /then go to NEGERR; if Lk= 1 /then go to POSERR; /SUM: =Ac; Ас: =0; /STOP; |
В случае если ветвление по знаку слагаемых не требуется, а необходимо только сигнализировать о переполнении, троичная программа сложения двух чисел с учетом их знаков допускает дальнейшее сокращение:
| START, | CLA CLL TAD А TAD В SZLS JMP OVRFLW DCA SUM HLT |
/Ас: =0; Lk: =0; /Ас: =Ac+A; /Ас: =Ac+B; /if Lk=0 /then go to OVRFLW; /SUM: =Ac; Ас: =0; /STOP; |
Эта программа, как и следовало ожидать, в точности совпадает с программой, реализующей на PDP-8 сложение чисел без знаков.
Рассмотренные примеры убедительно демонстрируют высокую эффективность троичной арифметики. Троичная арифметика для чисел со знаком так же проста и эффективна, как двоичная арифметика для чисел без знака.
Литература
- Shаnnonc. Е.А Symmetrical notation for numbers. - "The American Mathematical Monthly", 1950, 57, N 2, р, 90 - 93,
- Reid J.B. Letter to the editor. - "Comm. ACM", 1960, 3, N 3, р. А12 - A13.
- Howden Р.F. Weigh-counting technique is faster then binary.- "Electronics", 1974, 48, N 24, р. 121 - 122.
- Байцер Б. Архитектура вычислительных комплексов, т. 1. М., "Мир", 1974.
- Proceedings of the Sixth International Symposium on Multiple-Valued Logic, Мау 25 - 28 1976. IEEE Press, 1976.
- Croisier А. Introduction to pseudoternary transmission codes.- "IBM Journal of Research and Development", 1970, 14, N 4, р. 354 - 367.
- Брусенцов Н.П. Электромагнитные цифровые устройства с однопроводной передачей трехзначных сигналов. - В кн.: Магнитные элементы автоматики и вычислительной техники. XIV Всесоюзное совещание (Москва, сентябрь 1972 г.). М., "Наука", 1972, с. 242 - 244.
- Аристотель. 06 истолковании. СПб., 1891.
- Брусенцов Н.П. Диаграммы Льюиса Кэррола и аристотелева силлогистика. - В кн.: Вычислительная техника и вопросы кибернетики, вып. 13. Изд-во МГУ, 1976, с. 164-182.
- Introduction to programming. PDP-8 handbook series. Digital Equipment Corporation, 1972.
