Компьютер Фибоначчи

Алексей Стахов

От редакции.

Производительность, которая провозглашается сейчас как главное потребительское свойство современного процессора, безусловно, важна, но, на наш взгляд, все чаще более важным фактором становится его архитектура. Наращивание производительности — это типичное для американской инженерной школы применение метода грубой силы при решении проблемы. Для русской школы характерна глубокая научная проработка вопроса, позволяющая находить принципиально новые решения. Одно из таких решений описано в данной статье.

Эдуард Пройдаков.

Часть 1. Роль систем счисления в истории компьютеров

В предисловии к книге Анри Лебега “Измерение величин” академик А.Н. Колмогоров замечает: “У математиков существует склонность, уже владея законченной математической теорией, стыдиться ее происхождения. По сравнению с кристаллической ясностью развития теории, начиная с уже готовых ее основных понятий и допущений, кажется грязным и неприятным занятием копаться в происхождении этих основных понятий и допущений. Все здание школьной алгебры и весь математический анализ могут быть воздвигнуты на понятии действительного числа без всякого упоминания об измерении конкретных величин (длин, площадей, промежутков времени и т. д.). Поэтому на разных ступенях обучения с разной степенью смелости неизменно проявляется одна и та же тенденция: возможно скорее разделаться с введением чисел и дальше уже говорить только о числах и соотношениях между ними. Против этой тенденции и протестует Лебег”.

К сожалению, нечто подобное иногда наблюдается и в компьютерной науке. Владея развитой компьютерной теорией, компьютерные специалисты иногда забывают о той роли, которую сыграли системы счисления в истории компьютеров. Ведь первые счетные приборы (абаки и арифмометры), прообразы современных компьютеров, начали создаваться задолго до возникновения алгебры логики, теории алгоритмов — и главную роль при их создании сыграли именно системы счисления. Об этом не следует забывать, прогнозируя дальнейшее развитие компьютерной техники.

В истории систем счисления выделяют несколько этапов: начальная стадия счета, непозиционные системы счисления, алфавитные системы нумерации, поместные или позиционные системы счисления. Начальная стадия счета “характеризуется изображением сосчитываемых множеств при помощи частей тела, особенно пальцев рук и ног, палочек, узлов веревки и т.д. Как подчеркивается в статье И. Г. Башмаковой. и А. П. Юшкевича “Происхождение систем счисления” (“Энциклопедия элементарной математики”, том 1, “Арифметика”, 1951 г.), “…несмотря на крайнюю примитивность этого способа изображения, он сыграл исключительную роль в развитии понятия числа”. И именно в этот начальный период было сделано одно из крупнейших открытий античной математики. Речь идет о позиционном принципе представления чисел. Как подчеркивается в упомянутой выше статье Башмаковой И.Г. и Юшкевича А.П., “первой известной нам системой счисления, основанной на поместном, или позиционном принципе, является шестидесятеричная система древних вавилонян, возникшая примерно за 2000 лет до н. э.”.

Для объяснения вопроса о ее происхождении в истории математики возникло несколько конкурирующих гипотез. М. Кантор первоначально предположил, что сумерийцы (первичное население долины Евфрата) считали год равным 360 суткам и что шестидесятеричная система имеет астрономическое происхождение. По гипотезе Г. Кевича в долине Евфрата встретились два народа, из которых у одного была десятичная система счисления, а у другого основанием было число 6 (возникновение такого основания Кевич объясняет особым счетом на пальцах, в котором сжатая в кулак рука означала 6). Благодаря слиянию обеих систем возникло компромиссное основание 60. Заметим, что гипотезы Кантора и Кевича касаются вопроса о происхождении основания 60, но не самого позиционного принципа представления чисел.

На последний вопрос отвечает гипотеза Нейгебауера об измерительном происхождении позиционного принципа, изложенная в книге “Лекции по истории античных математических наук” (Т. 1. “Догреческая математика”. 1937). Согласно этой гипотезе “основные этапы образования позиционной системы в Вавилоне были таковы: (1) установление количественного соотношения между двумя самостоятельными существовавшими системами мер и (2) опускание названий разрядовых единиц при письме”. Эти этапы возникновения позиционных систем Нейгебауэр считает совершенно общими, подчеркивая при этом, что “позиционная шестидесятеричная система… оказалась вполне естественным конечным результатом долгого развития, ничем принципиально не отличающегося от аналогичных процессов в других культурах”.

Что касается основания 60, которое, по мнению Нейгебауэра, возникло как синтез вавилонских систем мер, то более убедительной все же является гипотеза Кантора о его “астрономическом” происхождении. Происхождение числа 60 в качестве основания вавилонской системы счисления, а также чисел 12, 30 и 360 как узловых чисел всех календарных систем, систем измерения времени и угловых величин можно объяснить с позиций астрологических и астрономических знаний и основанных на них представлений о гармонии Вселенной. В Вавилоне и Египте с давних времен при составлении календарей большое значение придавали самой крупной из планет-гигантов – Юпитеру, который примерно за 12 лет делает полный оборот вокруг Солнца. Не меньшую роль играл также Сатурн, который совершает полный оборот вокруг Солнца примерно за 30 лет. Приняв 60 лет в качестве главного цикла Солнечной системы, составителям древних календарей удалось идеально согласовать циклы Юпитера (5´12=60) и Сатурна (2´30=60).

Гармонию Вселенной с давних времен символизировали пять “правильных” геометрических тел, называемых “платоновыми телами”. Особую роль при этом играл додекаэдр – правильный двенадцатигранник, гранями которого являются правильные  пятиугольники (“пентаграммы”). Отсюда следует, что число углов на поверхности додекаэдра равно 5´12=60 (что соответствует 60-летнему циклу). Додекаэдр имеет 30 ребер (что соответствует циклу Сатурна) и 12 граней (что соответствует циклу Юпитера), а произведение этих чисел 30´12=360. Следуя магической числовой символике додекаэдра, которая отражала числовую гармонию циклов Юпитера и Сатурна, древние вавилоняне и выбрали число 60 в качестве основания своей системы счисления, а древние египтяне пришли к мысли разбить год на 12 месяцев (число граней додекаэдра), каждый из которых содержал ровно 30 дней (число ребер додекаэдра). Таким и был египетский календарь, созданный в IV тысячелетии до н.э. В этом календаре год состоял из 365 дней. Он делился на 12 месяцев по 30 дней каждый, в конце года добавлялось пять праздничных дней, которые, однако, не входили в состав месяцев. Заметим, что в своей системе измерения времени и угловых величин египтяне также использовали “магические числа” додекаэдра [1 сутки = 24 (2´12) часа, 1 час = 60 минут, 1 минута = 60 секунд, 2π=360°, 1°=60'].

Появление позиционной системы обозначения чисел считается одной из основных вех в истории материальной культуры. В ее создании принимали участие целые народы. В 6 в. н. э. подобная система возникла у племени майя. Наиболее распространено мнение, что основанием системы счисления майя является число 20, имеющее “пальцевое” происхождение. Однако известно, что в системе майя есть одно отступление от двадцатеричного основания. Вес следующего за узловым числом 20 индейцы майя выбрали равным 360 (а не 400). Все последующие веса разрядов являются производными от чисел 20 и 360, которые и выступают в роли “узловых чисел”, образующих систему майя. Как подчеркивается в упомянутой выше статье  Башмаковой И. Г. и Юшкевича А. П., это “объясняется тем, что год майя делили на 18 месяцев по 20 дней в каждом плюс еще пять дней”.  Таким образом, как и основание вавилонской системы, узловые числа системы майя имеют астрономическое происхождение. Существенно подчеркнуть, что годовой календарь майя по своей структуре (360+5) совпадал с египетским. Учитывая высокий уровень развития культуры майя, можно высказать предположение, что майя были знакомы с “платоновыми телами” и что их годовой календарь был связан с икосаэдром – правильным телом, двойственным додекаэдру. Икосаэдр представляет собой правильный двадцатигранник, гранями которого были правильные треугольники (отсюда деление месяца на 20 дней в календаре майя и выбор числа 20 в качестве первого узлового числа их  системы счисления). Икосаэдр имеет 30 ребер (как и у додекаэдра) и 12 вершин (30´12=360). В каждой вершине сходится 5 углов, т. е. общее число  углов на поверхности икосаэдра равно 5´12=60. Таким образом, числовые характеристики икосаэдра также связаны с 12-, 30- и 60-летними циклами Солнечной системы.

Мы для повседневных вычислений используем десятичную систему счисления, предшественницей которой является индусская десятичная система, возникшая примерно в XII-м столетии нашей эры. Известный французский математик Лаплас (1749—1827) выразил свое восхищение позиционным принципом и десятичной системой в следующих словах:

“Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этой методе, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой”.

Лаплас (1749—1827)

Убежденным сторонником использования индо-арабской десятичной системы счисления в торговой практике был известный итальянский математик Леонардо Пизанский (Фибоначчи), получивший математическое образование в арабских странах. В своем сочинении “Liber abaci” (1202) он писал:

“Девять индусских знаков — суть следующие: 9, 8, 7, 6, 5, 4, 3, 2, 1. С помощью этих знаков и знака 0, который называется по-арабски zephirum, можно написать какое угодно число”.

Здесь словом “zephirum” Фибоначчи передал арабское “as-sifr”, являющееся дословным переводом индусского слова “sunya”, то есть “пустое”, служившее названием нуля. Слово “zephirum” дало начало французскому и итальянскому слову “zero” (нуль). С другой стороны, то же арабское слово “as-sifr” было передано через “ziffer”, откуда произошли французское слово “chiffre”, немецкое “ziffer”, английское “cipher” и русское “цифра”.

Леонардо Пизано Фибоначчи (1170—1228)

Что касается выбора числа 10 в качестве основания десятичной системы счисления, то существует общепринятое мнение, что оно имеет “пальцевое” происхождение. Однако не следует забывать, что в древней науке число 10 всегда несло в себе особую смысловую нагрузку. Пифагорейцы называли его четверицей или тетрактидой. Говоря словами Эмпедокла в нем — “вечно текущей природы … корень источный”. Четверица 10=1+2+3+4 считалась у пифагорейцев одной из высших ценностей и являлась “символом всей Вселенной”, так как содержала в себе четыре “основных элемента”: единицу или “монаду”, обозначающую, по Пифагору, дух, из которого проистекает весь видимый мир; двойку, или “диаду” (2=1+1), символизирующую материальный атом; тройку, или “триаду” (3=2+1), то есть символ живого мира; и наконец, четверку, или “тетрада”, (4=3+1), соединявшую живой мир с монадой и поэтому символизировала целое, то есть “видимое и невидимое”. А поскольку тетрактида 10=1+2+3+4, то она выражала собой “Все”. Таким образом, гипотеза о “гармоничном” происхождении числа 10 имеет не меньшее право на существование, как и “пальцевая”.

В современной науке с развитием компьютерной техники на первые роли выдвинулась двоичная система счисления. Ее зачатки наблюдаются у многих народов. Например, у древних египтян широкое распространение получили методы умножения и деления, основанные на принципе удвоения. Изобретение двоичного способа нумерации приписывают китайскому императору Фо Ги, жизнь которого относится к 4-му тысячелетию до новой эры. Оказывается, к открытию двоичной системы счисления имели отношение многие математики, в частности, Фибоначчи. В своей книге “Liber abaci” он сформулировал “задачу о выборе наилучшей системы весовых гирь для взвешивания грузов на рычажных весах”. В русской историко-математической литературе эта задача известна под названием Баше—Менделеева в честь французского математика 17-го века Баше де Мезириака, поместившего ее в своем “Сборнике приятных и занимательных задач” (1612 г.), и выдающегося русского химика Дмитрия Ивановича Менделеева, который к концу жизни стал директором Главной Палаты мер и весов России и интересовался этой задачей по долгу своей службы.

Известно два варианта решения задачи Баше—Менделеева. Первый предполагает, что гири разрешается класть только на одну, свободную от груза чашу весов; при этом оптимальным решением является “двоичная система гирь”: 1, 2, 4, 8, 16,…, которая при взвешивании “порождает” двоичный способ представления чисел. При втором варианте гири разрешается класть на обе чаши весов; оптимальным решением при этом является “троичная система гирь”: 1, 3, 9, 27,…, которая при взвешивании “порождает” троичную симметричную систему счисления, которая и была положена Н. П. Брусенцовым в основу троичного компьютера “Сетунь”.

Но автор двоичной арифметики в истории науки доподлинно известен: это известный немецкий математик Лейбниц (1646-1716), который в 1697 г. разработал правила двоичной арифметики. Лейбниц настолько был восхищен своим открытием, что в его честь выпустил специальную медаль, на которой были даны двоичные изображения начального ряда натуральных чисел — возможно, это был тот редкий случай в истории математики, когда математическое открытие было удостоено такой высокой почести.

Лейбниц (1646—1716)

Лейбниц, однако, не рекомендовал двоичную арифметику для практических вычислений вместо десятичной системы, но подчеркивал, что “вычисление с помощью двоек, то есть 0 и 1, в вознаграждение его длиннот является для науки основным и порождает новые открытия, которые оказываются полезными впоследствии, даже в практике чисел, а особенно в геометрии: причиной чего служит то обстоятельство, что при сведении чисел к простейшим началам, каковы 0 и 1, всюду выявляется чудесный порядок”.

Блестящие предсказания Лейбница сбылись только через два с половиной столетия, когда выдающийся американский ученый, физик и математик Джон фон Нейман предложил использовать именно “двоичную” систему счисления в качестве универсального способа кодирования информации в электронных компьютерах (“Принципы Джона фон Неймана”).

Джон фон Нейман (1903—1957)

Таким образом, как подчеркивают многие выдающиеся математики, открытие вавилонянами позиционного принципа, а затем индусами десятичной системы счисления, основанной на позиционном принципе, а также разработку Лейбницем двоичной арифметики по праву можно отнести к разряду действительно эпохальных математических открытий, существенно повлиявших на развитие материальной культуры, в частности, на развитие компьютерной техники.

Почему же в теории чисел и в теоретической арифметике системам счисления не уделялось того внимания, которого они несомненно заслуживали? Все дело — в традиции. В античной науке, достигшей высокого уровня развития, впервые произошло сохранившееся до наших дней разделение математики на “высшую” куда относились геометрия и теория чисел, и “логистику” — прикладную науку о технике арифметических вычислений (“школьная” арифметика), геометрических измерениях и построениях. Уже со времени Платона логистика третировалась как низшая, прикладная дисциплина, не входящая в круг образования философа и ученого. Восходящее к Платону пренебрежительное отношение к школьной арифметике и ее проблемам, а также отсутствие какой-либо достаточно серьезной потребности в создании новых систем счисления в практике вычислений, которая в течение последних столетий всецело удовлетворялась десятичной системой, а в последние десятилетия — двоичной системой (в информатике), может служить объяснением того факта, что в теории чисел системам счисления не уделялось должного внимания и в этой части она не намного ушла вперед по сравнению с периодом своего зарождения.

Ситуация резко изменилась после появления современных компьютеров. Именно в этой области опять проявился интерес к способам представления чисел и новым компьютерным арифметикам. Все дело в том, что классическая двоичная система счисления обладает рядом принципиальных недостатков, главными из которых являются: проблема представления отрицательных чисел и “нулевая” избыточность классического двоичного способа представления чисел.

Особенно неприятен второй недостаток. “Нулевая” избыточность двоичного представления означает, что в системе счисления отсутствует механизм обнаружения ошибок, которые, к сожалению, неизбежно возникают в компьютерных системах под влиянием внешних и внутренних факторов. В условиях, когда человечество все больше становится заложником компьютерной революции и все чаще полагается на компьютер при решении сложнейших задач управления ракетами, самолетами, атомными реакторами, вопрос об эффективных механизмах обнаружения ошибок выдвигается на передний план. Ясно, что компьютеры, основанные на двоичной системе счисления, не всегда могут эффективно решать эту проблему.

Чтобы преодолеть указанные недостатки двоичной системы, уже на этапе зарождения компьютерной эры был выполнен ряд проектов и сделано несколько интересных математических открытий, связанных с системами счисления. Пожалуй, наиболее интересным проектом в этом отношении является троичный компьютер “Сетунь”, разработанный в Московском университете под руководством Н. П. Брусенцова. Использование в нем так называемой троичной симметричной системы счисления для представления чисел впервые в истории компьютеров поставило знак равенства между отрицательными и положительными числами, позволив отказаться от различных “ухищрений” (обратный и дополнительный код), используемых для представления отрицательных чисел. Это обстоятельство, а также использование “троичной логики” при создании программ привело к созданию весьма совершенной архитектуры, которая и была воплощена в модели “Сетуни”. Именно “Сетунь” является наиболее ярким историческим примером, подтверждающим влияние системы счисления на архитектуру компьютера!

Однако на заре компьютерной эры было сделано еще два открытия в области позиционных способов представления чисел, которые, однако, мало известны и которые в тот период не привлекли особого внимания математиков и инженеров.

В 1939 г. бельгийский врач Эдуард Цекендорф, увлекавшийся числами Фибоначчи, опубликовал статью, посвященную так называемым “суммам Цекендорфа”. Под представлением Фибоначчи—Цекендорфа понимается следующий позиционный способ представления чисел:

N = an F (n) + an-1F (n-1) + ... + ai F (i) + ... + a1F (1) (1)

где aiÎ{0, 1} — двоичная цифра i-го разряда представления; n — разрядность представления; F(i) — число Фибоначчи, задаваемое с помощью следующего рекуррентного соотношения:

F(i) = F(i-1) + F(i-2);
F(1) + F(2) = 1.

Однако наиболее революционным предложением в современной теории систем счисления по праву можно считать систему счисления с иррациональным основанием, предложенную в 1957 г. американским математиком Джорджем Бергманом. Под “Тау-системой”, или системой Бергмана понимается следующий способ представления действительного числа А:

(2)

где ai — двоичные цифры, 0 или 1; i = 0, ±1, ±2, ±3; ti — вес i-й цифры в представлении; t — основание системы счисления.

На первый взгляд может показаться, что в система Бергмана не представляет собой ничего особенного по сравнению с традиционным позиционным представлением, но это только на первый взгляд. Вся суть состоит именно в том, что основанием системы счисления является знаменитое иррациональное число t = которое является корнем следующего алгебраического уравнения:

x² = x + 1.

Будучи корнем указанного алгебраического уравнения, “золотая пропорция” обладает следующим математическим свойством:

tⁿ = t^n-1 + t^n-2,

где nпринимает значения из следующего множества: 0, ±1, ±2, ±3, … .

Именно в этом обстоятельстве (иррациональное основание t) кроется причина ряда “экзотических” свойств “системы Бергмана” (более подробно о ней можно узнать на Web-сайте “Музей Гармонии и Золотого Сечения”, (http://www.goldenmuseum.zibys.com/).

Существенно подчеркнуть, что “Тау-система” переворачивает наши традиционные представления о системах счисления, более того — традиционное соотношение между числами рациональными и иррациональными. В “Тау-системе” основанием, то есть началом счисления, является некоторое иррациональное отношение t, с помощью которого, используя систему (2) можно представить все другие числа, включая натуральные, дробные и иррациональные.

Идеи Цекендорфа и Бергмана получили дальнейшее развитие в работах автора настоящей статьи. В книге “Введение в алгоритмическую теорию измерения” (1977 г.) представление Фибоначчи—Цекендорфа” было обобщено с помощью понятия р-кода Фибоначчи, основанного на р-числах Фибоначчи, и разработана арифметика Фибоначчи для таких представлений.

Под р-кодом Фибоначчи понимается следующий способ представления натурального числа N:

N = anFp(n) + an-1Fp(n-1) + ... + aiFp(i) + ... + a1Fp(1) (3)

где aiÎ{0, 1} — двоичная цифра i-го разряда представления; n — разрядность представления; Fp(i) — р-число Фибоначчи, задаваемое с помощью следующей рекуррентной формулы:

F_р(i) = F_р(i-1) + F_р(i -р-1)  (4)

F_р(1) = F_р(2) = … = F_р(р+1) = 1   (5)

где р — целое неотрицательное число, принимающее значение из множества {0, 1, 2, 3,. ..}.

Заметим, что понятие “р-кода Фибоначчи” включает в себя бесконечное число представлений, так как каждому р соответствует свое представление; при этом для случая р=0 р-код Фибоначчи вырождается в классическое двоичное представление, а для случая р=1 — в представление Фибоначчи—Цекендорфа. При р=¥ любое р-число Фибоначчи равно 1, а это означает, что р-код Фибоначчи сводится к так называемому “унитарному коду”:

N = 1 + 1 + … + 1

А это, в свою очередь, означает, что р-коды Фибоначчи как бы заполняют пробел между классической двоичной системой счисления и унитарным кодом, включая их в качестве частных крайних случаев.

В книге “Коды золотой пропорции” (1984 г.) с использованием так называемых обобщенных золотых пропорций была обобщена система счисления Бергмана. Такие способы представления чисел были названы кодами золотой пропорции.

Под кодами золотой пропорции понимаются следующие способы представления действительного числа А:

  (6)

где ai — двоичные цифры, 0 или 1; i = 0, ±1, ±2, ±3; – вес i-й цифры в представлении; tр — “золотая р-пропорция”, являющаяся действительным корнем следующего алгебраического уравнения:

x^p+1 = x^p + 1,

где целое число р принимает значение из множества {0, 1, 2, 3,. ..}.

Заметим, что при р=0 уравнение золотой р-пропорции вырождается в тривиальное уравнение x=2, и при этом tр = 2; при р=1 оно вырождается в уравнение для классической золотой пропорции и корень tр совпадает с классической золотой пропорцией.

Будучи корнем указанного алгебраического уравнения, “золотая р-пропорция” обладает следующим математическим свойством:

,

где nпринимает значения из следующего множества: 0, ±1, ±2, ±3,…

Заметим, что код золотой пропорции (6) является весьма широким обобщением классической двоичной системы счисления (случай р=0) и системы Бергмана (р=1). При р=¥ код золотой пропорции сводится к “унитарному коду”.

Таким образом, р-коды Фибоначчи (3) и коды золотой р-пропорции (6) есть не что иное, как весьма широкое обобщение классического двоичного представления. Для представления чисел они используют те же двоичные символы 0 и 1 и по форме представления ничем не отличаются от классического двоичного кода. Различие между ними возникает только на этапе интерпретации весов двоичных разрядов. Например, одна и та же комбинация двоичных знаков 1001101 представляет в двоичной системе счисления различные числа, а именно число 45 = 2⁶ + 2³ + 2² + 2⁰ в классической двоичной системе счисления, число 19 = 13 + 3 + 2 + 1 в коде Фибоначчи (1) и число А = t⁶ + t³ + t² + t⁰ — в “Тау-системе” (2), где t =  — золотая пропорция. Заметим, что число А является иррациональным числом! А это означает, что в “Тау-системе” мы можем представлять некоторые иррациональные числа в виде конечной совокупности битов! В этом и состоит первый неожиданный результат, вытекающий из теории кодов золотой пропорции.

Основное преимущество кодов Фибоначчи и кодов золотой пропорции для практических применений состоит в их “естественной” избыточности, которая может быть использована для целей контроля числовых преобразований. Эта избыточность проявляет себя в свойстве “множественности” представлений одного и того же числа. Например, число 19 в коде Фибоначчи имеет и другие кодовые представления:

19 = 1001101 = 1010001 = 1010010 = 0111101.

При этом различные кодовые представления одного и того же числа могут быть получены одно из другого с помощью специальных фибоначчиевых операций “свертки” (011®100) и “развертки” (100®011), выполняемых над кодовым изображением числа. Если над кодовым изображением выполнить все возможные “свертки”, то мы придем к специальному фибоначчиевому изображению называемому “минимальной формой”, в которой двух единиц рядом в кодовом изображении не встречается. Если же в кодовом изображении выполнить все возможные операции “развертки”, то придем к специальному “фибоначчиевому” изображению, называемому “максимальной”, или “развернутой” формой, в которой рядом не встречается двух нулей.

Именно эти математические результаты стали основой для проектов создания компьютерных и измерительных систем на основе “фибоначчиевого” и “золотого” представлений.

Часть вторая. Краткая история работ по компьютеру Фибоначчи в СССР

Изложенные в первой части статьи математические результаты стали основой для проектов создания компьютерных и измерительных систем на основе “фибоначчиевого” и “золотого” представлений. Эти проекты выполнялись в Советском Союзе в 1970-е и 1980-е годы. По решению Госкомизобретений изобретения в области компьютеров Фибоначчи были запатентованы за рубежом. Таким образом, 65 зарубежных патентов США, Японии, Англии, ФРГ, Франции, Канады и других стран и свыше 100 авторских свидетельств СССР являются официальными юридическими документами, подтверждающими приоритет советской науки в разработке данной темы. И хотя создать компьютер Фибоначчи так и не удалось (основной причиной тому стал развал Советского Союза и связанное с этим прекращение финансирования исследовательских работ), теоретические основы данного направления представляют несомненный интерес и могут стать источником новых идей не только в компьютерной области, но и в области математики. Особенно эффективным автор считает использование “фибоначчиевых” представлений в измерительной технике и цифровой обработке сигналов, где с их помощью в последние годы были разработаны сверхбыстрые сигнальные преобразования.

А начиналось это так. Вечером 3 марта 1976 г. в семинарской комнате Австрийского кибернетического общества (Вена, Шотенгассе, 3) было весьма многолюдно. Известные австрийские ученые, члены кибернетического и компьютерного обществ Австрии, научные сотрудники компьютерной лаборатории американской фирмы IBM в Вене и представители посольства СССР собрались в семинарской комнате. Главной причиной этого необычного собрания была лекция “Алгоритмическая теория измерения и основания компьютерной арифметики”. Читал ее автор настоящей статьи Алексей Стахов, в ту пору заведующий кафедрой информационно-измерительной техники Таганрогского радиотехнического института. Однако были различные причины, которые собрали вместе известных ученых в области кибернетики и информатики и сотрудников советского посольства. Объявление о лекции провозглашало следующее:

“Методы представления чисел могут быть рассмотрены как специальные алгоритмы измерения. Такая интерпретация является главной идеей лекции.

Основные научные результаты:

• новый научный принцип, “Принцип асимметрии измерений”;
• алгоритмическая теория измерения;
• расширение теории чисел Фибоначчи;
• фибоначчиева арифметика как способ повышения информационной надежности компьютерных систем”.

Таким образом, главная цель лекции состояла в том, чтобы изложить новую теорию — “алгоритмическую теорию измерения”, вытекающие из нее новые способы позиционного представления чисел и новую компьютерную “арифметику Фибоначчи”, которая может быть положена в основу компьютеров Фибоначчи, нового направления в развитии компьютеров.

Интерес советского посольства к этой лекции носил политический характер. Дело в том, что 5 марта 1976 г., то есть спустя два дня после нее, в Москве должно было состояться открытие 25-го съезда КПСС. А несколькими месяцами ранее известный западногерманский журнал Spiegel опубликовал очень острую статью “Если б Ленин это знал!”. Статья была посвящена фактам коррупции в высших эшелонах КПСС. И тогда ЦК КПСС направил во все советские посольства в западных странах секретный меморандум, рекомендовавший способствовать выступлениям в этих странах советских артистов, спортсменов и ученых, чтобы хоть как-то сгладить негативное впечатление мировой общественности от публикации в журнале Spiegel.

Весьма положительные отзывы, которые дали о лекции известные австрийские ученые (президент Австрийского кибернетического общества проф. Трапель, директор Института обработки данных Венского технического университета проф. Эйер, а также представитель кафедры статистики и информатики Линцского университета имени Иоганна Кеплера проф. Адам), вызвали в посольстве СССР в Австрии естественное желание посодействовать развитию этого направления и в Советском Союзе. Посол И. Ефремов направил в Государственный комитет Совета Министров СССР по науке и технике и в Министерство высшего и среднего специального образования СССР соответствующее письмо.

Следствием письма посла было решение Госкомизобретений о патентовании изобретения проф. Стахова во всех ведущих странах — продуцентах средств вычислительной техники.

Как известно, для получения зарубежного патента оформляется соответствующая заявка на изобретение с учетом требований патентного ведомства той или иной страны, и эта заявка подается в данное ведомство с ходатайством выдать патент на изобретение. Надо отметить, что ни в одной стране патентное ведомство не заинтересовано в выдаче такого патента, потому что это ущемит права собственных производителей; поэтому проводится весьма тщательная патентная экспертиза, которая во многих случаях заканчивается отказом в выдаче патента. При этом все услуги по патентованию (даже в случае отрицательного решения) оплачивает страна, ходатайствующая о выдаче патента. Вот почему решения о патентовании советских изобретений за рубежом (особенно в области электроники и вычислительной техники) принимались только в исключительных случаях и осуществлялись на государственном уровне. Однако в соответствии с патентными законами большинства стран невозможно получить патент на математическое изобретение, каким, в сущности, и была фибоначчиева арифметика. И тогда возникла мысль о косвенной защите этой арифметики через компьютерные устройства, ее реализующие. Такими устройствами являются регистры, счетчики, сумматоры, множительные и делительные устройства и т. д., то есть основные операционные устройства компьютера Фибоначчи. При этом желательно было придумать такой оригинальный операционный элемент, который мог бы потянуть на пионерное изобретение, на основе которого можно было бы создать все остальные операционные элементы.

Анализ фибоначчиевой арифметики (см. www.goldenmuseum.zibys.com) показал, что основными ее операциями являются так называемые “свертка”, “развертка” и основанная на них операция приведения кода Фибоначчи к минимальной форме. Именно поэтому главным объектом патентной защиты стал новый операционный элемент компьютерной техники, названный устройством приведения кода Фибоначчи к минимальной форме (см. врезку).

Несмотря на предельную простоту устройства (см. рисунок), оно не имело прототипов по своему функциональному назначению и было признано в СССР и в других странах изобретением пионерного характера. Затем были разработаны другие операционные элементы компьютера Фибоначчи (в частности, счетчики и сумматоры). Это также были новые элементы компьютерной техники, но они не были пионерными изобретениями, поскольку основывались на устройстве приведения кода Фибоначчи к минимальной форме.

С экономической точки зрения (стоимость патентования) выгоднее патентовать заявку на изобретение с так называемой многозвенной формулой. По существу речь шла о такой крупномасштабной заявке, которая включала бы в себя несколько десятков технических решений, объединенных общей идеей и общей формулой изобретения. Такой и была первая заявка на изобретение компьютера Фибоначчи: она содержала свыше 200 страниц текстового материала, около 100 рисунков (операционные устройства и их элементы), а многозвенная формула изобретения состояла из 85 пунктов, описывала 85 технических решений, то есть 85 изобретений. Всего же к патентованию было принято 12 заявок.

Патентование осуществлялось в восьми странах (США, Япония, Англия, Франция, ФРГ, Канада, Польша и ГДР). Для этого каждая из 12 заявок составлялась с учетом патентного закона каждой страны и затем переводилась на соответствующий язык.

Итоги патентования “фибоначчиевых” изобретений превзошли все ожидания: 65 зарубежных патентов, выданных патентными ведомствами США, Японии, Англии, Франции, ФРГ, Канады, Польши и ГДР свидетельствует о том, что идея компьютера Фибоначчи имеет мировую новизну, так как западная патентная экспертиза не сумела ничего противопоставить советским “фибоначчиевым” изобретениям.

Специальное конструкторско-технологическое бюро “Модуль”

К сожалению, сами по себе патенты еще ничего не означали. Для того чтобы получить экономические выгоды от патентования, в частности от продажи лицензий на эти патенты, срочно требовалась реализация изобретений в виде некоторых систем и устройств, которые по своим параметрам должны были превосходить мировой уровень. Такая задача была поставлена перед автором со стороны Госкомизобретений СССР, который нес государственную ответственность за патентование и прикладывал максимум усилий, чтобы сдвинуть с мертвой точки “проблему внедрения”.

В 1977 г. автор был избран на должность заведующего кафедрой вычислительной техники Винницкого политехнического института, и именно этот вуз стал основным научным центром, где были развернуты работы по реализации изобретений. Сложность состояла еще и в том, что направление начало развиваться не в одном из признанных советских компьютерных центров (Москва, Киев, Минск), а в украинской Виннице, “сахарной” столице Украины, где хотя и были электронные заводы, но их целевая направленность и уровень технологии явно не соответствовали задаче создания компьютера Фибоначчи. Да и сам институт находился в стадии роста, шли бесконечные дрязги в профессорском коллективе — и все это не способствовало развитию этого научного направления.

В 1986 г. Минвуз Украины по настоянию Госкомизобретений назначил автора директором специального конструкторско-технологического бюро “Модуль”, входившего в состав Винницкого политехнического института. Оно имело несколько отделов конструкторского направления и некоторую технологическую базу, но находилось на грани финансового краха. Поэтому первоочередной задачей было найти устойчивый источник финансирования разработок. Решить ее удалось за короткий срок благодаря поддержке этого научного направления прежде всего со стороны Госкомизобретений, а также некоторых высокопоставленных чиновников бывшего СССР. В Киеве таким чиновником оказался Владимир Павлович Горбулин, занимавший пост заместителя начальника оборонного отдела ЦК Компартии Украины, в Москве — Олег Федорович Антуфьев, начальник одного из ведущих главков Министерства общего машиностроения (МОМ) СССР (советского ракетного министерства). Именно по инициативе этих двух прогрессивно мысливших советских функционеров работы по компьютеру Фибоначчи были включены в одно из секретных постановлений ЦК КПСС и СМ СССР по развитию оборонной тематики. В результате на разработки было выделено около 15 млн. рублей — значительная для того времени сумма, втрое превышавшая годовой объем финансирования научно-исследовательских работ всего Винницкого политехнического института.

Заказчиком, в качестве которого выступала головная компьютерная организация МОМ, было сформулировано три основных направления научных и опытно-конструкторских разработок:

• проектирование самоконтролирующегося процессора Фибоначчи для специальных применений;
• проектирование самокорректирующихся “фибоначчиевых” аналого-цифровых и цифро-аналоговых преобразователей высокой точности и метрологической стабильности;
• проектирование самосинхронизирующихся систем цифровой магнитной записи и волоконно-оптических систем передачи информации.

К этим разработкам в СКТБ было подключено около 200 сотрудников.

Первая микросхема

Одним из важнейших направлений инженерных разработок СКТБ “Модуль” стало создание элементной базы компьютеров Фибоначчи, на чем особенно настаивал “заказчик”. В перспективе планировалось, что такая элементная база станет основой для проектирования бортового высоконадежного компьютера Фибоначчи (Ф-компьютера) для специальных применений.

Первой была разработана микросхема небольшой разрядности, выполняющая функции процессора. Несколько таких микросхем в совокупности представляли процессор Ф-компьютера более высокой разрядности.

Устройство приведения кода Фибоначчи к минимальной форме

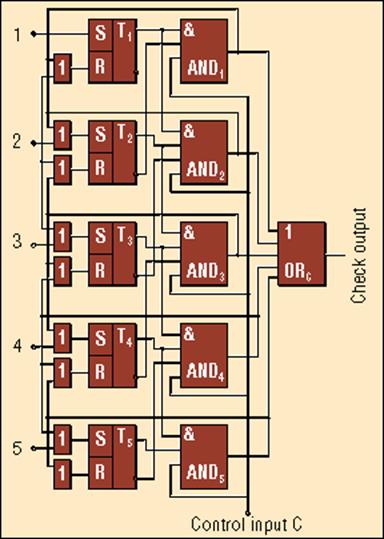
Один из возможных вариантов такого устройства показан на рисунке. Устройство состоит из пяти R-S-триггеров и логических элементов AND, OR(И, ИЛИ), которые предназначены для реализации “свертки”. Операция “свертки” выполняется, начиная с младшего триггера T₁ к старшему триггеру T₅, с помощью логических элементов AND₁ — AND₅ и соответствующих логических элементов OR (ИЛИ), расположенных перед R- и С-входами соответствующих триггеров. Логический элемент AND1 реализует “свертку” 1-го разряда во 2-й разряд регистра. Два его входа связаны с прямым выходом триггера T₁ и “инверсным” выходом триггера T₂. Третий вход связан с сигналом синхронизации C. Логический элемент AND₁ анализирует состояния Q₁ и Q₂ триггеров T₁ и T₂. Если Q₁ = 1 и Q₂ = 0, это означает, что условие “свертки” для 1-го и 2-го разрядов выполняется. Синхросигнал C = 1 является причиной появления логической 1 на выходе элемента AND₁. Эта логическая 1 вызывает переключение триггеров T₁ и T₂ в противоположное состояние, что приводит к выполнению операции “свертки” над первыми двумя разрядами регистра.

Логический элемент AND_kk-го разряда (k = 2, 3, 4, 5) реализует операцию “свертки” (k – 1)-го и k-го разрядов в (k+ 1)-й разряд. Три его входа связаны с “прямыми” выходами триггеров T_k–1 и T_k и “инверсным” выходом триггера T_k+1. Четвертый вход связан с синхросигналом C. Логический элемент AND_k анализирует состояния Q_k-1, Q_k и Q_k+1 триггеров T_k-1, T_k и T_k+1. Если Q_k-1 = 1, Q_k= 1 и Q_k+1 = 0, это означает, что условие “свертки” выполняется. Синхросигнал C= 1 приводит к переключению триггеров T_k-1, T_k, и T_k+1. При этом выполняется операция “свертки” над соответствующими разрядами (011 ® 100).

Заметим, что все элементы AND₁ — AND₅ связаны через общий логический элемент ORc с контрольным выходом регистра “свертки”.

Устройство, изображенное на рисунке, работает следующим образом. Входная кодовая информация поступает на входы 1—5 устройства и далее — на S-входы триггеров через соответствующие логические элементы OR.

Устройство приведения кода Фибоначчи к минимальной форме

Пусть исходное состояние регистра, составляющего основу устройства, следующее:

5 4 3 2 1

0 1 0 1 1

Ясно, что условие “свертки” выполняется только для 1-го, 2-го и 3-го разрядов. Синхросигнал C= 1 приводит к переходу регистра в следующее состояние:

5 4 3 2 1

0 1 1 0 0

Здесь условие “свертки” выполняется только для 3-го, 4-го и 5-го разрядов. Очередной синхросигнал C= 1 приводит к переходу регистра в следующее состояние:

5 4 3 2 1

1 0 0 0 0

Приведение исходной кодовой комбинации 0 1 0 1 1 к “минимальной форме” закончилось.

Итак, в предыдущей части мы остановились на том, что была выпущена микросхема, в основу которой положена арифметика Фибоначчи, построенная на так называемых “базовых микрооперациях”. Как известно, компьютерная программа реализуется с помощью процессора (ЦП), состоящего из триггеров, связанных с комбинационной логикой. Таким образом, исполнение программы сводится к переключению триггеров. К сожалению, невозможно полностью исключить ошибки, возникающие в результате неисправной работы компьютерных элементов. Но при этом необходимо различать два типа неисправностей. Первый тип называется постоянным отказом элемента, когда однажды отказавший элемент “выбывает из игры”, а второй -- случайным отказом (или сбоем), когда элемент отказывает в случайные моменты времени, а остальное время работает корректно. Сбои в работе процессора возникают под влиянием различных факторов, вызываемых внешними и внутренними шумами в компьютерных элементах и их электронных цепях.

Какой вид неисправной работы наиболее характерен для электронных элементов? Установлено, что сбои в этих элементах, в частности в триггерах, возникают чаще, чем постоянные отказы. Существует два режима работы электронных элементов: 1) режим, когда элемент находится в стабильном (устойчивом) состоянии, и 2) режим переключения, когда элемент переключается из одного устойчивого состояния в другое. Экспериментально доказано, что интенсивность сбоев триггеров во втором режиме на 2--3 порядка больше, чем в первом. Отсюда вытекает, что сбои триггеров в режиме переключения являются наиболее вероятной причиной ненадежного функционирования процессоров. Вот почему проектирование самоконтролирующихся цифровых автоматов, гарантирующих эффективный контроль сбоев триггеров, — одна из важнейших проблем проектирования высоконадежных процессоров.

Таким образом мы пришли к идее создания процессора, позволяющего обнаруживать сбои триггеров, возникающие в момент их переключения. Мы будем называть его помехоустойчивым процессором.

Суть подхода к созданию такого процессора состоит в следующем. Необходимо выбрать набор микроопераций, называемых базовыми,на основе которых может быть реализован любой алгоритм обработки информации, и затем ввести эффективную систему их схемного контроля.      Покажем возможность реализации этой идеи на основе “фибоначчиевой” и “золотой” систем счисления. С этой целью рассмотрим четыре базовые микрооперации: a) свертка; б) развертка; в) перемещение; г) поглощение.

Напомним, что свертка и развертка представляют собой следующие кодовые преобразования, выполняемые в рамках одного и того же “фибоначчиевого” или “золотого” представления:

свертка:

0 1 1 ® 1 0 0

развертка:

1 0 0 ® 0 1 1

Микрооперация перемещение является двуместной микрооперацией и реализуется над одним и тем же разрядом двух регистров: верхнего регистра Aи нижнего регистра B. Если регистр Aимеет двоичную цифру 1 в k-м разряде, а регистр B — двоичную цифру 0 в том же самом разряде, мы можем реализовать микрооперацию перемещения. Это означает, что мы передвигаем цифру 1 из верхнего регистра Aв нижний регистр B:

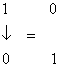
Микрооперация поглощение также является двуместной операцией и состоит в том, что две двоичные цифры 1 одного и того же разряда регистров A и B взаимно уничтожаются, то есть заменяются двоичными цифрами 0:

1          0

  =

1          0

(О том, как из перечисленных микроопераций строятся операции сложения и вычитания, а также доказывается их помехозащищенность, можно узнать из полной версии статьи на сайте компьютерного музея www.computer-museum.ru. — Прим. ред.)

Мы доказали, что базовые микрооперации обладают функциональной полнотой, т. е. к ним могут быть сведены все возможные логические и арифметические операции. Следовательно, мы можем проектировать полностью помехозащищенный Ф-процессор и компьютер на основе базовых микроопераций.

К сожалению, СКТБ “Модуль” не имело специальных САПР и поэтому проектирование велось сотрудниками СКТБ с использованием САПР НПО “Научный центр” (г. Зеленоград). Там же изготовили 100 опытных образцов такой микросхемы на основе БИС КР 1801 ВП1-124.

В микросхеме была заложена возможность выполнения следующих операций: запись и чтение данных, свертка, развертка, перемещение, поглощение, приведение к минимальной форме, суммирование, вычитание, реверсивный сдвиг, логическое умножение, логическое сложение и сложение по модулю 2. Все указанные операции контролировались в соответствии с вышеуказанным принципом.

Отличительной особенностью микросхемы являлось наличие контрольного выхода, на котором формировалась информация о неправильной работе микросхемы. Одновременно с выдачей сигнала “ошибка” блокировались все информационные выходы. Если ошибка была следствием сбоя и при повторении операции сигнал “ошибка” не появлялся, то блокировка выходов снималась. Если же внутри микросхемы происходил отказ, то блокировка информационных выходов оставалась.

Таким образом, основным результатом этой разработки было создание первой в истории компьютерной техники микросхемы для реализации самоконтролирующегося процессора Фибоначчи со 100%-ной гарантией обнаружения сбоев, возникающих при переключении триггеров.

“Фибоначчиевые” система регистрации и волоконно-оптическая линия связи

 В 1965 г. американский инженер Кауц (Kautz) опубликовал статью “Fibonacci Codes for SynchronizationControl” в весьма престижном международном журнале IEEE Trans. IT (1965, v.11, № 2). В ней обсуждалась еще одна область весьма эффективного применения кодов Фибоначчи — управление синхронизацией кодовых сигналов в каналах связи и в цифровой магнитной записи. Это направление исследований также получило отражение в разработках СКТБ “Модуль”. Первая из них — волоконно-оптическая линия связи повышенной пропускной способности. При этом в системе использовалось два способа кодирования информации, так называемый бифазный код типа “Манчестер” и код Фибоначчи.

Приведенные ниже технические характеристики волоконно-оптических систем связи, построенных на различных системах кодирования, свидетельствуют о неоспоримых преимуществах кода Фибоначчи.

Технические характеристики волоконно-оптической системы связи:

Скорость передачи информации, Мбит/с
бифазный код  — 10
код Фибоначчи —  20

Вероятность ошибки в канале
бифазный код — 10-9
код Фибоначчи — 10-11
Максимальная длина линии связи — 1000

Однако наиболее широкую известность получили инженерные разработки СКТБ “Модуль” по проектированию самокорректирующихся “фибоначчиевых” аналого-цифровых и цифро-аналоговых преобразователей. Этим разработкам предшествовала большая научная работа. По тематике “фибоначчиевых” АЦП и ЦАП в тот период было защищено наибольшее число кандидатских диссертаций (Азаров, Марценюк, Петросюк, Моисеев, Стейскал, Крупельницкий). Эти исследования убедительно показали, что применение кодов Фибоначчи и “золотой” позволяет одновременно улучшить все технические параметры АЦП и ЦАП, в частности точность, быстродействие и, самое главное, температурную и временную метрологическую стабильность АЦП и ЦАП.

Как известно, в АЦП и ЦАП, построенных на основе классической двоичной системы счисления, возможно появление “разрывов” передаточной характеристики, которые могут возникнуть в результате отклонения от номинальных значений резисторов двоичного делителя, реализующего веса двоичных разрядов. В “фибоначчиевых” АЦП и ЦАП “разрыв” передаточной характеристики автоматически исключается за счет многозначности Ф-представления одной и той же величины. Все “фибоначчиевые” разряды разбиваются на группу старших разрядов, отклонения которых от номинальных значений приводит к существенному влиянию на погрешность преобразования, и группу младших разрядов, незначительно влияющих на погрешность преобразования. Если теперь под влиянием технологических, температурных или временных факторов (старение элементов) происходят отклонения значений резисторов старших разрядов от номинальных значений, то, кодируя одну и ту же величину дважды (с включенным и выключенным старшим разрядом), по разности результатов кодирования можно определить отклонение старшего разряда от номинального значения. Если эту же процедуру выполнить для следующего по старшинству разряда, то можно также вычислить отклонение очередного старшего разряда от собственного номинального значения. Такая корректирующая процедура производится в “фибоначчиевом” АЦП перед каждым его включением, что позволяет каждый раз как бы восстанавливать его точность. Теоретические и экспериментальные исследования показали, что отклонения резистивных элементов от своих номинальных значений могут быть весьма существенными (до 23%); при этом путем коррекции погрешность АЦП и ЦАП может быть снижена в 1000 раз и более. В реальных разработках допускалась погрешность резистивных элементов в 5%, а погрешность АЦП и ЦАП при этом соответствовала 0,005% и ниже. Таким образом, в Ф-АЦП и Ф-ЦАП резко снижались требования к технологической точности изготовления резистивного делителя. Кроме того, если под влиянием температуры или старения происходили отклонения элементов резистивного делителя от номинальных значений, то они также корректировались с помощью описанной выше процедуры. В результате достигалось весьма существенное преимущество — Ф-АЦП и Ф-ЦАП оказывались нечувствительными к технологии изготовления, температуре и старению.

Свойство многозначности Ф-представления давало еще один весьма существенный эффект при борьбе с так называемыми “динамическими” погрешностями, вызванными инерционностью включения резистивных элементов, моделирующих веса разрядов. Была разработана специальная процедура кодирования, которая исключению таких динамических погрешностей. Это позволило существенно повысить тактовую частоту кодирования, что дало повышение быстродействия Ф-АЦП примерно в 5--6 раз по сравнению с двоичным АЦП, построенном на такой же элементной базе.

Было создано несколько модификаций таких АЦП и ЦАП, выпускавшихся в мелкосерийном производстве. Однако в условиях межведомственной борьбы в бывшем СССР добиться промышленного выпуска данных изделий не удалось (см. электронную версию статьи).

К сожалению, горбачевская “перестройка” привела к существенному сокращению финансирования научных разработок, которые проводились в оборонных целях. В 1989 г. МОМ СССР сообщило о прекращении финансирования работ по созданию компьютера Фибоначчи. Это привело к развалу научного и инженерного коллектива, сформировавшегося в СКТБ “Модуль”.

Теоретические исследования однако в данном направлении не прекратились. В последнее десятилетие автором настоящей статьи получен ряд фундаментальных результатов в развитии “фибоначчиевой” информатики и математики: разработана троичная зеркально-симметричная арифметика; развита теория матриц Фибоначчи и на этой основе предложена новая теория кодирования и криптографии.

Что делается за рубежом по “фибоначчиевому” направлению?

Необходимо отметить большой интерес американских математиков к “фибоначчиевому” направлению. Для развития теории чисел Фибоначчи в 1963 г. группа американских математиков, возглавляемая Вернером Хоггаттом, организовала математическую Фибоначчи-Ассоциацию, которая выпускает журнал The Fibonacci Quarterly и ежегодно с 1984 г. Проводит международную конференцию “Fibonacci Numbers and their applications”. Все это стимулировало развитие данного направления в современной математике. И в области теории чисел Фибоначчи американская математика в настоящее время несомненно лидирует. Пожалуй, наиболее важным теоретическим достижением в области нетрадиционных систем счисления является статья американского математика Джорджа Бергмана “A number system with an irrational base” (Mathematics Magazine, 1957, № 31). В 1965 г. была опубликована статья американского инженера Kautz W.H. “Fibonacci codes foe synchronization control” (IEEE Trans. Inform. Theory, v.11, № 8). Эта идея была развита в СКТБ “Модуль” и Киевском НПО “Маяк”.

Что касается компьютеров Фибоначчи, то здесь также имеется несколько американских публикаций, свидетельствующих о том, что работы по этому направлению в США проводились. В статье “Minimal and maximal Fibonacci Representations: Boolean Generation”, опубликованной P. Monteiro и R. Newcomb (University of Maryland) в журнале The Fibonacci Quarterly (1976, v. 14, № 1), описывается устройство для приведения кода Фибоначчи к минимальной форме, которое стало предметом советского патентования примерно в то же время. В статье отмечается, что эта работа была поддержана отделом научных исследований ВВС США в соответствии с грантом AFOSR 70-1910, откуда следует, что эта разработка проводилась в военных целях. Характерна статья “Multilevel Fibonacci Conversion and Addition”, опубликованная P. Licomendes и R. Newcomb (University of Maryland) в журнале The Fibonacci Quarterly (1984, v. 22, № 3). В ней описывается способ преобразования двоичного представления Фибоначчи в троичное представление Фибоначчи. В статье имеется ряд ссылок на другие публикации.

Из этого далеко не полного перечня публикаций американских ученых можно сделать вывод, что понятие “компьютер Фибоначчи” прочно вошло в американскую компьютерную литературу и что работы по этим компьютерам проводились в США (Университет шт. Мэриленд) примерно в тот же период, что и работы по “фибоначчиевому” направлению, выполнявшиеся под руководством автора настоящей статьи сначала в Таганрогском радиотехническом институте (1971—1977 гг.), где началось зарубежное патентование компьютера Фибоначчи, а затем в Винницком политехническом институте (в период с 1977 по 1990 гг).

Из последних приложений кодов Фибоначчи следует упомянуть такую важную область информатики, как цифровая обработка сигналов. В российской науке идеи использования чисел Фибоначчи для создания сверхбыстрых алгоритмов цифровой обработки активно развивает доктор физико-математических наук профессор Владимир Михайлович Чернов (Самара, Институт обработки изображений РАН). Подобные же исследования проводятся в Финляндии (Tampere International Center for Signal Processing). Исследования в области “фибоначчиевых” сигнальных преобразований изложены в книге “Fibonacci Decision Diagram“ (2000 г.) авторов R. S. Stankovic, M. Stankovic, J. T. Astola, K. Egizarian. В ней широко используются так называемые обобщенные числа Фибоначчи (р-числа Фибоначчи), введенные автором настоящей статьи еще в 1975 г. Сверхбыстрые “фибоначчиевые” преобразования могут быть реализованы только над числовыми данными, представленными в р-кодах Фибоначчи. Это означает, что для реализации таких преобразований требуется создание специализированных процессоров Фибоначчи!

В появившемся в конце года оценочной плате для сигнального процессора семейства ADSP-2189М фирмы Analog Devices, в частности, указывается: “Демонстрационные программы, поставляемые в составе этого комплекта, включают алгоритмы обработки сигналов, такие, как свертка и вычисления в кодах Фибоначчи”. Подробнее информацию о плате можно получить по адресам: http://www.analog.com/dsp/tools/design.html, http://www.analog.com/industry/dsp/tools/. История повторяется, и она нас, славян, к сожалению, ничему не научила. Как говорил первый президент Украины Леонид Кравчук, “маемо те, що маемо”.

Статья опубликована в PC Week/RE №№32, 34, 35, 2002 г. с незначительным сокращением.
Статья переведена в html-формат 11.09.2009 г.