Исчерпывающее решение «неодолимой» проблемы парадоксов

Брусенцов Н. П.

Формальная логика, величающая себя наукой о правильном мышлении, в действительности препятствует освоению человеком взаимосвязанности реальных вещей. Достаточно сказать, что в современной логике непредставима первейшая фундаментальная взаимосвязь – отношение необходимого следования, без которого неосуществимо адекватное умозаключение, невозможна безупречная логика реальности.

Противоестественность общепринятой ныне двухзначной логики заложена в самой её первооснове – догматическом законе исключённого третьего, введённом античными стоиками вопреки диалектической трёхзначности силлогистики Аристотеля. Общеутвердительная аристотелева силлогистическая посылка “Все x суть y” представляет собой именно то следование с необходимостью y из x , которое в условиях навязанной стоиками двухзначности выродилось в парадоксальную “материальную импликацию”. Согласно двухзначной импликации из несуществующего следует всё, что угодно, а необходимо существующее следует из чего угодно. Это явно несовместимо с интуитивным пониманием следования, со здравым смыслом.

Проблема устранения парадоксов обрела первостепенное значение уже в средние века и особенно в последнее столетие с появлением алгебры логики, но устранить их так и не удалось – логика, даже математическая, все ещё лишена способности доказательно умозаключать, в ней отсутствует отношение необходимого следования.

Поразительно, что внедрённая вопреки Аристотелю двухзначность была затем неоправданно присвоена логике самого Аристотеля. Поэтому устранять парадоксы пытаются главным образом путём изобретения “неаристотелевых” логик, что заведомо недостижимо, поскольку непарадоксальность свойственна именно аристотелевой силлогистике. Странно, ведь о трёхзначности силлогистики чётко сказано в самом определении отношения следования [1, “Первая аналитика”, 57b], где, наряду с противоположностями “необходимо есть” и “необходимо нет”, указано диалектическое третье – “не необходимо есть” (оно же – “не необходимо нет”). Именно это представленное в силлогистике частными посылками третье сообщает силлогистическим взаимосвязям естественную изменчивость, предотвращающую возникновение парадоксов.

Для постижения сущности непарадоксального необходимого следования нет нужды изобретать неаристотелевы импликации, подобно Лукасевичу, который, не разглядев трёхзначности у Аристотеля, изобрёл свою трёхзначную логику, увы, не решившую проблемы. Трёхзначные импликации, предложенные интуиционистами и иными логиками, также не достигли цели – трёхзначность хотя и необходимое, но не достаточное условие адекватности. Подлинное начало непарадоксальной логики может быть достоверно установлено исследованием того, как осуществлено необходимое следование в силлогистике.

Неотобразимость аристотелевой силлогистики в современных логических исчислениях высказываний и предикатов дала повод неоправданно квалифицировать её “как узкую систему, неприменимую ко всем видам рассуждений, например, к математическим доказательствам” [2, с.189]. Но ведь то, что непарадоксальная силлогистика непостижима в парадоксальных исчислениях – неопровержимое свидетельство вовсе не её “узости”, а очевидной неполноценности этих исчислений. Для уразумения силлогистики необходимо прежде всего придать естественность и безупречность самому логико-алгебраическому исчислению.

Структура общепринятого ныне исчисления предикатов восходит к введённому Аристотелем в “Категориях” истолкованию первичных сущностей как сущностей единичных вещей [1, 2a1]. Это предопределило экстенсиональный, родо-видовой характер исчисления. Впоследствии, в “Метафизике”, Аристотель признал благоразумным противоположное: “... поскольку мы каждую вещь познаем через определения, а начала определений – это роды, необходимо, чтобы роды были началами и определяемого...” [1, 998b4]. Однако, эта интенсиональная трактовка не была воплощена в силлогистике и всё ещё не воспринята логикой.

Пожалуй, единственным примером осуществления предусмотренной Аристотелем коррекции является “Символическая логика” Льюиса Кэррола [3], упорно отвергаемая всей традиционной наукой, отстаивающей свой нелепый закон исключенного третьего, несмотря на порожденные им парадоксы.

В логике Кэррола первичными терминами x, y, z,... обозначены не единичные вещи, а элементарные качества, присущность либо антиприсущность которых составляют особенности вещи, так что сущности вещей выражаются совокупностями их особенностей относительно рассматриваемых качеств-терминов.

Алгебраически различаемые относительно n первичных качеств вещи представимы n -терминными элементарными конъюнкциями, в которые термины, именующие присущие данной вещи качества входят непосредственно (неинвертированными), антиприсущие качества-термины отмечаются штрихом (инвертируются), а несущественные для определяемой вещи (вернее, для неединичного класса вещей), упускаются, “умалчиваются”.

Например четырёхугольники, различаемые относительно качеств: прямоугольность – x, равносторонность – y, обретающих в составе конъюнкции значения особенностей охарактеризованной конъюнкцией вещи, оказываются следующих видов: xy – прямоугольный и равносторонний (квадрат), x – прямоугольник, xy' – неравносторонний прямоугольник, y – ромб, x'y' – непрямоугольный и неравносторонний четырёхугольник.

В отличие от двухзначной логики высказываний и предикатов, у Кэррола третье несущественное принято не только для особенностей, совокупностями которых определены вещи, но и для самих вещей, совокупностями которых отображены суждения и их алгебраические эквивалентны, выражающие логические взаимосвязи. Позиции диаграммы Кэррола, сопоставленные (так же как на таблице истинности Пирса) вещам, наряду с принятыми в двухзначной логике значениями “1” и “0” (“необходимо есть”, “необходимо нет”) допускают третье – “не необходимо есть/нет”. У Кэррола символами значений служат красная и чёрная фишки, означающие соответственно: “необходимо существует” и “не существует” (“невозможно”). Третье значение – “не необходимо существует” (“может быть, а может не быть”) представлено отсутствием фишки – существование вещи, сопоставленной незанятой позиции, не утверждается и не отрицается. На приводимых здесь рисунках красной фишкой служит плюс, а чёрной минус.

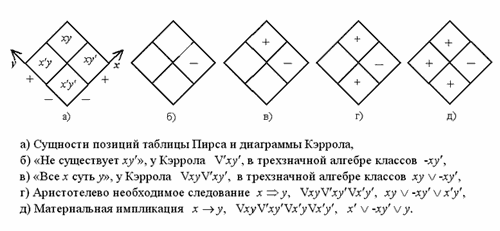
Кэррол установил, что не всем отобразимым на его диаграмме совокупностям вещей соответствуют суждения, выражающие реально осуществимые взаимосвязи, поскольку не все мыслимое и выразимое на языке алгебры возможно в действительности. Как пример такого нереального суждения (суждения-химеры) он приводит [3, с. 255] представленное на диаграмме одной чёрной xy -фишкой суждение «Ни один xy не существует». Три аналогичных суждения с одной черной фишкой xy' , x'y либо x'y' также химеры. В частности, одна чёрная xy' – фишка отображает “строгую импликацию” Льюиса, якобы непарадоксальную.

Кэррол полагал реальным суждение “Все x суть y”, отображаемое сочетанием xy' -чёрной и xy -красной фишек. Но оно также химера, ибо не утверждает существования x' и y'. Реальность же достигается добавлением ещё и x'y' -красной фишки, обеспечивающим безукоризненное отображение необходимого следования x ⇒ y [4].

Отображающая это фундаментальное отношение совокупность вещей, наряду с несуществованием xy' -вещей и существованием с необходимостью xy -вещей и x'y' -вещей, включает x'y -вещи в третьем статусе – как не необходимо существующие (могут быть, могут не быть). Это убедительно свидетельствует о невозможности необходимого следования в условиях неосмотрительно положенного в основание логики закона исключённого третьего.

Трёзначность отменяет пагубный закон, открывая возможность реставрировать здравое мышление, но та же попытка отобразить суждение “Все x суть y” трёхзначной диаграммой с одной красной и одной чёрной фишками показывает, что только трёзначностью химеры неустранимы. Поэтому и ни одна из изобретёных в поисках отношения следования трёхзначных импликаций следованием не оказалась.

Однако в силлогистике Аристотеля то же общеутвердительное суждение “Все x суть y ” истолковывается именно как непарадоксальное необходимое следование y из x . Отношение это определено Аристотелем в «Первой аналитике» [1, с. 215]:

«… когда два [объекта] относятся друг к другу так, что если есть один, необходимо есть и второй, тогда, если нет второго, не будет и первого; однако если второй есть, то не необходимо, чтобы был первый. Но невозможно, чтобы одно и то же было необходимо и когда другое есть, и когда его нет».

“Объекты” здесь суть качества-термины: “первый” – x , “второй” – y . То, что y необходимо есть, когда есть x , как и то, что x не может быть когда нет y , означает несуществование xy' -вещей. Однако определяемое отношение оказывается непарадоксальным необходимым следованием y из x только при сосуществовании x -вещей и y' -вещей, т. е. при сосуществовании противоположностей по каждому из терминов: x и x', y и y'.

Силлогистика предполагает сосуществование противоположностей относительно каждого термина-качества. Ни одна из особенностей x, x', y, y', ... при этом не может быть ни общезначимой, ни противоречивой, поэтому ни парадоксы, ни химеры в аристотелевой силлогистике невозможны.

Сосуществование противоположностей – это принцип, положенный в основание логики Гераклитом, который призывал прислушиваться к голосу природы, а не придумывать несвойственные ей законы в духе омертвившего логику закона исключённого третьего. Противоположности “есть”, “нет” несовместимы, противоречивы, но они необходимо сосуществуют. Сущность качества x выявляется сопоставлением вещей, которым оно присуще ( x -вещей), с вещами, которым оно антиприсуще ( x' -вещами). Качество x реально, если сосуществуют x -вещи и x' -вещи, а иначе оно химера, и отношения с таким качеством заведомо будут парадоксальными.

Таким образом, парадоксы возникают в связи с нереальностью (общезначимостью или противоречивостью) содержащихся в суждении качеств-терминов. Непарадоксальность логики обеспечивается соблюденностью принципа сосуществования противоположностей, означающего также переменность терминов, на что ещё в 13-м веке указывал Дунс Скот. Ныне же именем его назван один из парадоксов материальной импликации.

Диаграмма Кэррола отображает множество (сосуществование) вещей, составляющих класс, представленный таблицей Пирса. Таблица истинности Пирса истолковывается как дизъюнкция, наиболее широкий класс (род), включенных в неё вещей, представленных каждая конъюнкцией её особенностей – присущности либо антиприсущности рассматриваемых качеств-терминов.

При трёхзначном обобщении алгебры логики умалчивание несущественных членов, общепринятое в конъюнкции, осуществляют и в дизъюнкции, введя вместо нынешнего исключения умалчиваемых членов, явно исключающий символ – знак минус. В такой - 0 + трёхзначной системе отношение материальной импликации x→y выразится в виде , а непредставимое в двухзначной логике непарадоксальное следование будет

Кэррол использует для множественного представления отображаемых его диаграммой совокупностей вещей и соответствующих взаимосвязей терминов изобретенный им “метод индексов” [3,с.255], в котором сущности вещей, представляемые обычно конъюнкциями терминов, выражены при помощи терминов с индексами 1 и 0. Но равнозначное множественное представление осуществимо и с привычным выражением сущностей вещей теми же конъюнкциями, что и в таблицах истинности, в сочетании с функтором существования, префикс-дизъюнкцией V. Конъюнкция таких существований/несуществований, а также умалчивание несущественных в отображаемом множестве вещей представляет собой множественное отображение их совокупности и определяемой ею взаимосвязанности терминов.

Например, материальная импликация x→y представима множеством , а непарадоксальное следование , где умалчиванием x'y -вещей отображена их несущественность для представляемой взаимосвязи.

Реальность (непарадоксальность) логики будь то в кэрроловом истолковании её на множествах взаимосвязанных вещей или в общепринятой ныне экстенсиональной трактовке как иерархии классов достигается непреклонным соблюдением первоосновы миропорядка – принципа сосуществования противоположностей.

Из 19683 двухтерминных трёхзначных отношений реальны только восемь:

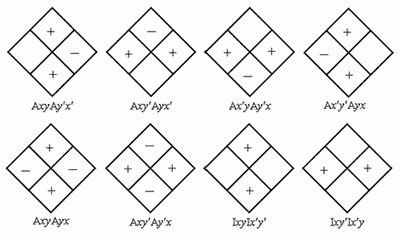
Здесь функторы A , I обозначают соответственно общеутвердительное и частноутвердительное суждения в традиционном (буквальном) истолковании. Общие же суждения непарадаксальной, соблюдающей гераклитов принцип силлогистики контрапозитивны:
, а частные – попарно инверсны, т.е. Ixy немыслимо без Ix'y', одно не существует без другого, по принципу сосуществования противоположностей, иначе парадоксы неустранимы.

В цитированном выше аристотелевом определении следования условие “если есть y, то не необходимо, чтобы был x” призвано предотвратить превращение в xy. Вместе с тем, если есть y, то не необходимо, чтобы был x', иначе термин y утрачивает переменность и возникает парадокс. В силлогистике это несовместимо с сосуществованием противоположностей, сохраняющимся, кстати, в двухзначном отношении тождества xy.

Однако следование трёхзначно: в нём, наряду с “необходимо есть” и “необходимо нет” имеет место умалчиваемое на диаграммах и в выражениях трёхзначной алгебры привходящее (x'y в случае следования ). Оно и есть то самое третье, исключив которое, логику лишили установленной Гераклитом и неукоснительно соблюдаемой Аристотелем диалектической естественности – того, что “прокладывает путь к началам всех учений” [1, с.351].

В итоге изложенного остается заключить, что начало реальной (диалектической) логики бытия не тождество и не единство, а сосуществование противоположностей, не конъюнкция, а исключающая дизъюнкция их. Сама суть противоположностей – сосуществование несовместимых, отвергающее исключение третьего.

Реставрации благоразумной логики посвящен наш сайт ternarycomp.cs.msu.ru

Литература

1. Аристотель. Сочинения в четырех томах. – М.: «Мысль», т. 1 – 1975, т. 2 – 1978.
2. Лукасевич Я. Аристотелевская силлогистика с точки зрения современной формальной логики. – М.: ИЛ, 1959.
3. Кэррол Л. Символическая логика // Льюис Кэррол. История с узелками. – М.: «Мир», 1973.
4. Брусенцов Н.П. Диаграммы Льюиса Кэррола и аристотелева силлогистика // “Вычислительная техника и вопросы кибернетики”, вып. 13. – М.: Изд-во Моск. ун-та, 1977. С. 164-182.

Заметки о трехзначной логике

Опубликовано: Фонд «Новое тысячелетие», 2008. – 8 с.
Публикуется с разрешения автора.
Помещена в музее 22.11.2008