Модели ЭГДА и сетки сопротивлений

А. Д. Смирнов

В 1919 г. русский ученый, академик Н. Н. Павловский, математически обосновал и применил метод электромоделирования для решения дифференциального уравнения Лапласа при расчете гидротехнических сооружений: плотин, дамб, шпунтовых стенок и т. п.

В тех немногих случаях, когда плотина строится в каменном ущелье, расчет плотины ведется из условий, чтобы напор воды не смог ее сдвинуть, опрокинуть или проломить. Но большинство рек нашего Союза, в особенности в европейской его части, протекают в песчаных, суглинистых или других водопроницаемых берегах. Вода, поднятая плотиной, под большим напором просачивается через такой грунт, размывает его и, если не принять предохранительных мер, может подмыть плотину и разрушить ее. Чтобы воспрепятствовать этому, стремятся искусственно увеличивать гидравлическое сопротивление слоя грунта под плотиной. Как мы выяснили из второго примера, разобранного в предыдущем параграфе, гидравлическое сопротивление тем больше, чем длиннее участок фильтрации. Для удлинения пути фильтрации воды под плотиной, выше и ниже плотины бетонируют дно (рис. 6, а). Помимо этого, под плотиной забивают в грунт несколько сплошных (глухих) заборов из металлических железобетонных или деревянных пластин, так называемых шпунтовых рядов.

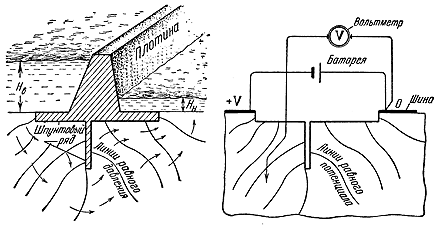
Рис. 6. Решение задачи о фильтрации воды под плотиной методом электромоделирования на установке ЭГДА: а - схема процесса, происходящего в натуре: H_В и H_Н – уровни воды выше и ниже плотины; стрелки показывают направление фильтрации; б - электрическая модель этого процесса.

Все эти элементы плотины требуют точного расчета; недостаточная прочность их может вызвать разрушение плотины, излишнее усиление — значительное удорожание строительства. А для расчета их необходимо знать, как меняется напор воды под плотиной, сколько воды, с какой скоростью и по какому пути будет просачиваться? При этом нужно рассчитать несколько вариантов, чтобы выбрать наилучший.

Для определения фильтрационных характеристик грунта на месте будущей плотины бурят скважины и берут пробы грунта. Составляют уравнение, решив которое можно получить величины напоров и скоростей. Но решение такого уравнения требует многих недель работы инженеров и техников-вычислителей. Физическое же моделирование такого сооружения сопряжено с большими трудностями. Где же выход из положения?

Ясно, что нужно попытаться построить такую электрическую модель этой задачи, чтобы уравнения, описывающие зависимости между расчетными гидравлическими величинами и между электрическими величинами в модели, были аналогичны.

Такой выход из положения и предложил академик Н. Н. Павловский. Водопроницаемый грунт он отобразил на модели листом станиоля (тонкопрокатным листовым оловом, такого типа, какой употреблялся в бумажных конденсаторах, и похожим на металлические обертки шоколада или чая).

По форме водонепроницаемых элементов плотины были сделаны вырезы в станиоле (рис. 6, б). Разность напоров между верхним и нижним бьефами моделировалась разностью потенциалов на питающих медных шинах. Так как основное движение грунтовых вод идет под плотиной, то участки дна, расположенные далеко от плотины, можно не моделировать. Такое ограничение области моделирования не скажется сильно на решении.

Уравнение для определения электрического потенциала в любой точке станиоля на модели и для определения напора воды в аналогичной точке под плотиной будут одинаковы.

Значит, можно, не решая уравнения, замерить вольтметром на модели потенциалы в различных точках и, умножив их на коэффициент пропорциональности, получить величины напоров под плотиной. (Линии равных напоров под плотиной и линии равных потенциалов будут геометрически подобны.) По силе тока определяется и секундный расход воды, протекающий под плотиной. Изменения, вносимые в конструкцию плотины, легко моделируются изменениями в форме вырезов в листе станиоля.

Вместо листа станиоля можно брать раствор электролита, — тогда вся установка выполняется в виде ванны.

В последние годы для этой же цели стали применять электропроводящую бумагу. Моделирующие установки с электропроводящей бумагой были сконструированы украинским ученым В. П. Фильчиковым и его сотрудниками.

Такая установка портативна, удобна в обращении и по размерам не превосходит письменного стола. Одним из важных свойств этой установки является наглядность получаемых результатов. Решение, получаемое путем замеров потенциалов, непосредственно заносится на эту же бумагу в форме линий равного потенциала или в числовой форме около каждой точки, в которой производилось измерение.

Н. Н. Павловский назвал этот метод моделирования ЭГДА, что значит электро-гидродинамическая аналогия. Это название сохранилось за подобными моделями, хотя решаются на них не только гидродинамические задачи, а любые задачи, сводящиеся к решению так называемого “уравнения Лапласа”: тепловые, гидродинамические, электростатические, магнитные и др.

Дальнейшее развитие метод Н. Н. Павловского получил в работах ленинградского математика С. А. Гершгорина, доказавшего, что непрерывную среду в модели: лист станиоля, раствор электролита или электропроводящую бумагу- можно заменить сеткой, составленной из отдельных сопротивлений.

Какую же выгоду дает такая замена? Для выяснения этого вернемся к задаче фильтрации воды под плотиной. Грунт под ней может быть неоднородным. Его гидравлическое сопротивление будет различным в разных местах. Значит, и на электрической модели его нужно изобразить средой с различным электрическим (омическим) сопротивлением, полностью повторяющим гидравлическое сопротивление грунтов. Например, в том месте, где в песчаном грунте встречается залегание пласта суглинка неправильной формы, в электрической модели, на участке подобной же формы, омическое сопротивление среды должно быть увеличенным.

На установках со станиолем или электропроводящей бумагой этого добиться очень трудно. На установках с жидким электролитом можно добиться этого, изменяя толщину слоя электролита за счет изменения профиля дна ванны. Там, где сопротивление должно быть меньше, дно ванны имеет углубление — толщина слоя электролита над этим местом делается больше, площадь поперечного сечения возрастает, омическое сопротивление уменьшается. Там, где требуется создать участок с повышенным сопротивлением, на дне ванны делается выпуклость. Чтобы легко менять конфигурацию дна, его делают из пластичного материала. Наряду с положительными свойствами — точным геометрическим подобием исследуемой области и непрерывностью получаемого решения — электролитическая ванна обладает и большими недостатками: она занимает много места, электролит со временем высыхает, при прохождении тока в нем возникают процессы электролиза, пузырьки водорода и кислорода, выделяясь на питающих шинах и иглах измерительного прибора, создают изоляционную пленку, которая нарушает их правильную работу.

От всех этих недостатков свободны модели-сетки. Сопротивление в сетках легко сделать переменным, выполнив их в виде миниатюрных магазинов сопротивлений или реостатов. Изменение сопротивлений внутри исследуемой области может быть произведено в течение короткого промежутка времени. Переход от одной задачи к другой или изменения, вводимые в ходе исследования одной задачи, легко выполняются путем подключения или отключения части сопротивлений или путем изменения места подвода питания и величины питающего напряжения или силы тока. Благодаря тому, что электрический ток в моделях-сетках можно подводить не только к питающим шинам, но и к любой точке сетки и изменять сопротивления по любому закону, на сетках можно моделировать более сложные дифференциальные уравнения, чем на установках типа ЭГДА. На сетке, правда, нельзя получить непрерывного решения, и для уточнения решения в отдельных местах приходится применять более частую сетку.

У нас в Советском Союзе  Л. И. Гутенмахером, Н. В. Корольковым, Н. С. Николаевым и др. создано несколько типов электромоделей сеток.

Глава из книги “Современные математические машины”, М., 1959 г., стр. 17.
Перепечатывается с разрешения автора.